【题解】CF538C

前言

第一篇在洛谷过审的题解！！！

原题链接

一些胡言乱语

校模拟赛出了这道题，考场上推出来式子但是没有特判首尾，于是挂了 30。

另外，这仿佛是我在洛谷的第一篇题解。

题意

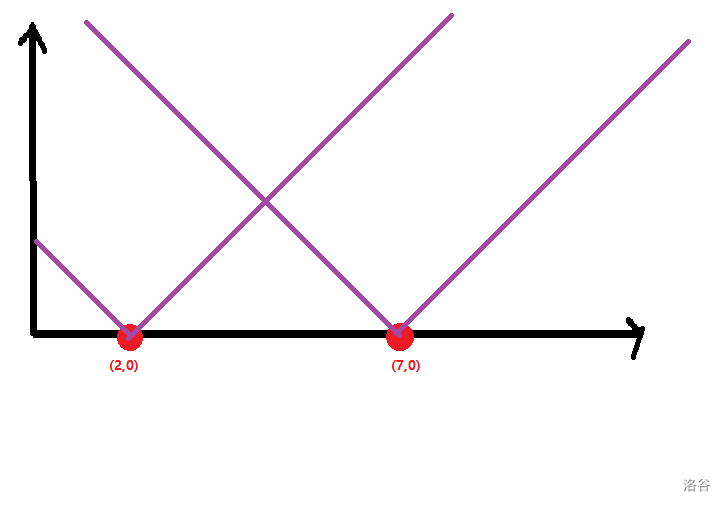
简化一下题意，实际上就是给定 $n$ 个点，由这 $n$ 个点引出斜率为 $\pm 1$ 的直线，求所有交点的最大值。

以样例 1 为例：

8 2
2 0
7 0

如果按照刚刚写的理解方式，画成一个平面就是：

推式子

肯定是要循环写的。

设一个 $A(d_i,h_i),B(d_{i+1},h_{i+1})$。

待定系数法，先设穿过 A 的直线为 $y_1=x_1+b_1$，求出来 $b_1=h_i-d_i$。

再设穿过 $B$ 的直线为 $y_2=-x_2+b_2$，求出来 $b_2=d_{i+1}+h_{i+1}$。

然后计算两直线交点，即 $-x+d_{i+1}+h_{i+1}=x+h_i-d_i$。

求出来 $x=\frac{d_{i+1}+h_{i+1}+d_i-h_i}{2}$。

所以此时得到的最大值就是 $\frac{d_{i+1}+h_{i+1}+d_i-h_i}{2}+h_i-d_i$。

循环的时候去 $\max$ 即可。

本题还要求判断无解，那么什么时候无解呢？就是两个点连成一条直线的斜率大于 1 的时候，即 $|\frac{h_{i+1}-h_i}{d_{i+1}-d_i}|>1$ 的情况。

另外首尾还需要特判一下。

AC 代码

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n,m;
struct node{
	int d,h;
}a[N];
int ans=-1;
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++) scanf("%d%d",&a[i].d,&a[i].h);
	ans=a[1].d+a[1].h-1;//首特判
	for(int i=1;i<m;i++){
		if(abs(a[i].h-a[i+1].h)>a[i+1].d-a[i].d){//判断无解
			printf("IMPOSSIBLE");
			return 0;
		}
		ans=max(ans,max(a[i].h,a[i+1].h)+((a[i+1].d-a[i].d)-abs(a[i].h-a[i+1].h))/2);
	}
	ans=max(ans,a[m].h+n-a[m].d);//尾特判
	printf("%d",ans);
}