【算法笔记】zkw线段树

zkw线段树

zkw线段树是一种用循环实现的线段树，比正常的递归式线段树快很多，而且好写。

zkw线段树的常数约为普通线段树的四分之一，在某些情况下比树状数组还快，有一次模拟赛，同机房大佬qidirj就用莫队套zkw线段树通过了一道用普通莫队套线段树只能得50分的题，这就是小常数的优势。

zkw线段树的引入

我们观察一个线段树的结构，按照堆式储存，叶子节点的序号是连续的。

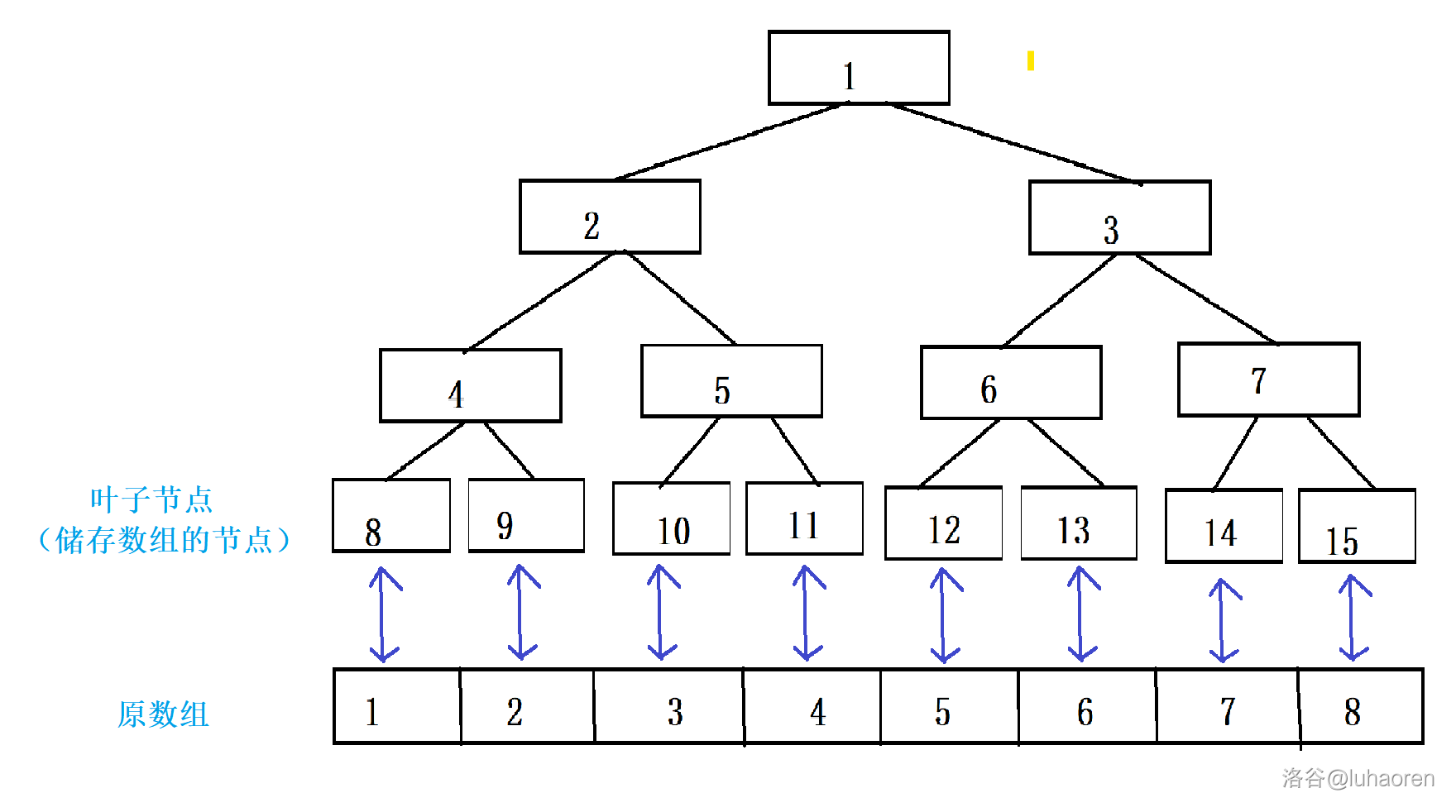
而原数组中的数字编号也恰恰是连续的，所以二者之间有一个对应关系。

仔细观察，发现两者序号之差竟然是一个定值。

所以，我们就可以快速地找到数字在线段树中的位置，即x+N（N为差值）。

而这个$N$就应该是线段树中抛去叶子节点之外的节点的数量。

为了方便，我们约定，无论树有没有那么大，我们都把$N$看作$n$，无数据的叶节点空置即可。

这样我们就可以通过循环的方式，完成线段树的初始化。

建树代码

int tr[N*4];//zkw线段树不用维护子区间，直接开数组就行
int n,m;
void build(){
	cin>>n>>m;
	for(int i=n+1;i<=2*n;i++) cin>>tr[i];//直接读入到叶子节点里
	for(int i=n-1;i>=1;i--) tr[i]=tr[i*2]+tr[i*2+1];//自底向上更新
}

建树才三行代码，还包括了读入，zkw线段树是不是很神奇？

单点修改&区间查询

单点修改

找到了数字在线段树中的位置，怎么更新它的父节点呢？

按照堆式储存的特点，节点的父节点就应该是$x/2$（x是这个节点）

那么从叶子节点开始，一步步地向上爬，更新，就完成了一次单点修改。

这也是zkw线段树的一个特色——自底向上。

单点修改代码

inline void change(int x,int k){//给x加上k
	for(int i=x+=n;i;i/=2) tr[i]+=k;//自底向上更新
}

看完单点修改，相信大家已经会了单点查询，那就是：

单点查询代码

inline int query_one(int x){//查询x值
	return tr[x+n];
}

区间查询

接下来思考，如何做到区间查询呢？

如图，以查询$[3,6]$区间之和为例，我们先设两个指针$p,q$，让$p=l-1,q=r+1$。

然后让$p$和$q$一直往上跳，直到两个指针的父节点相同。

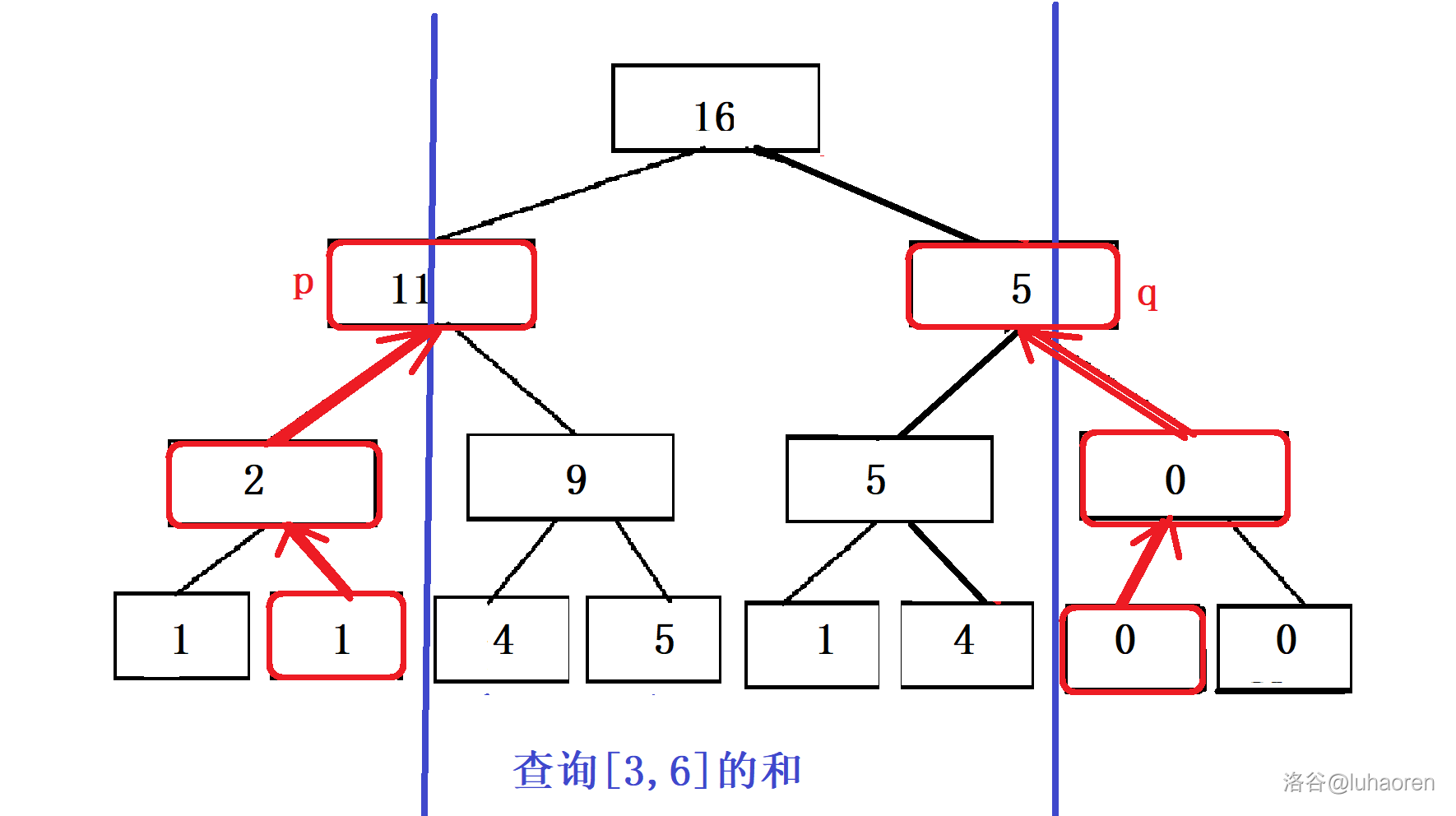
有没有发现，这两个指针笼罩的地方，就是我们要查询的区间。

我们会发现一个规律：

1. $p$指向的节点是左儿子，那么答案加上右儿子的值

2. $q$指向的节点是右儿子，那么答案加上左儿子的值

区间查询代码

inline int query(int l,int r){
	int ans=0;
	for(int p=l-1+n,q=r+1+n;p/2!=q/2;p/=2,q/=2){
		if(!(p%2)) ans+=tr[p+1];//第一种情况
		if(q%2) ans+=tr[q-1];//第二种情况
	}
	return ans;
}

习题

1. P3374 单点修改，区间查询 用zkw线段树再做一遍

区间修改&单点查询

区间修改

zkw线段树也支持区间修改，但是由于很难做到pushdown，所以zkw线段树采用标记永久化的方式进行区间修改。

区间修改和区间查询差不多，也是维护两个指针，不同点是：从累加答案变成修改懒标记。

区间修改代码

void uplate(int l,int r,int k){//给l,r区间内的数加上k
	for(int p=l-1+n,q=r+1+n;p/2!=q/2;p/=2,q/=2){
		if(!(p%2)) add[p+1]+=k;
		if(q%2) add[q-1]+=k;
	}
}

单点查询

在有懒标记的情况下，单点查询也变得不同。

首先自底向上累加所有祖宗节点的懒标记，然后再加上本身的值。

单点查询代码

inline int query_one(int x){//查询x值
	int sum=0;
	for(int i=x+=n;i;i/=2) sum+=add[i];
	return tr[x+n]+add[i];
}

习题

1. P3372 线段树1
   用zkw线段树做一遍
2. P3368 树状数组2
   区间修改，单点查询