【算法笔记】线段树基础

前言

线段树，是数据结构皇冠上的明珠（我编的）。

它用途广泛，被一代代的oier应用，改进，优化。

一个博客需要由一张头图

本文介绍了线段树的基础知识，希望能帮到更多的oier。

在学习线段树前，默认你应该学会一下内容：

树和二叉树的基本知识（这你总得会吧）
二叉堆（主要是堆式储存）
离散化（其实并不需要）
会写代码

如果你不会，左转oiwiki，如果你会，那么继续读吧！

线段树的引入

举个例子，我们现在有一个序列，想维护一段子区间的和，该怎么办呢？

你或许会说，可以暴力！把这个区间的数加起来就行了。

那么如果这个子区间里有 $10^5$ 个数呢？

前缀和？

如果强制在线呢？

如果在维护区间和的同时维护最大值、并且支持区间修改呢？

我们有很多种办法维护区间问题，比如树状数组，线段树，分块。其中，线段树是较通用且直观的一种数据结构。

基础线段树

线段树入门

首先，我们有一个序列。

\left \{ 1,1,4,5,1,4 \right \}

我们利用二分的思想，用每一个节点表示一个区间，两个子节点表示左右两个子区间。

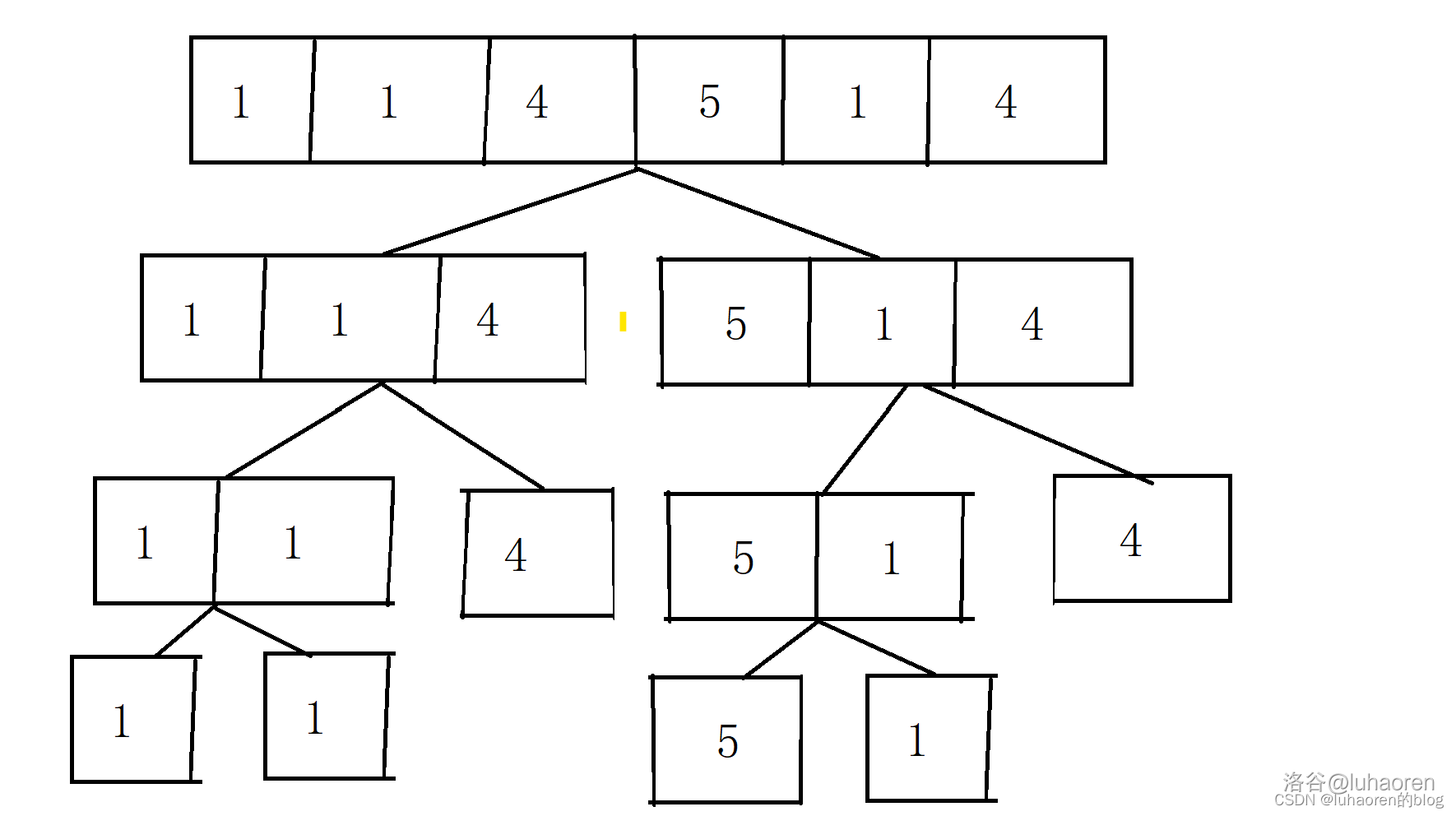
然后我们就可以在每个节点处维护一些信息。

注意：实际上，只有最下面一层的叶子节点才保存了实际的数字，其它的每个节点只保存着这个区间的信息（如区间和，区间最值等）

那么如何把子节点的信息传到父节点上呢？

我们要了解一个叫做 $pushup$ 的操作。

1
2
3

void pushup(int x){
	tr[x].sum=tr[x*2].sum+tr[x*2+1].sum;
}

这个操作的意思就是：节点表示的区间和等于两个子节点所表示的区间之和。即下图：

有了这个操作，我们就可以递归的求出每一个节点所表示的信息。

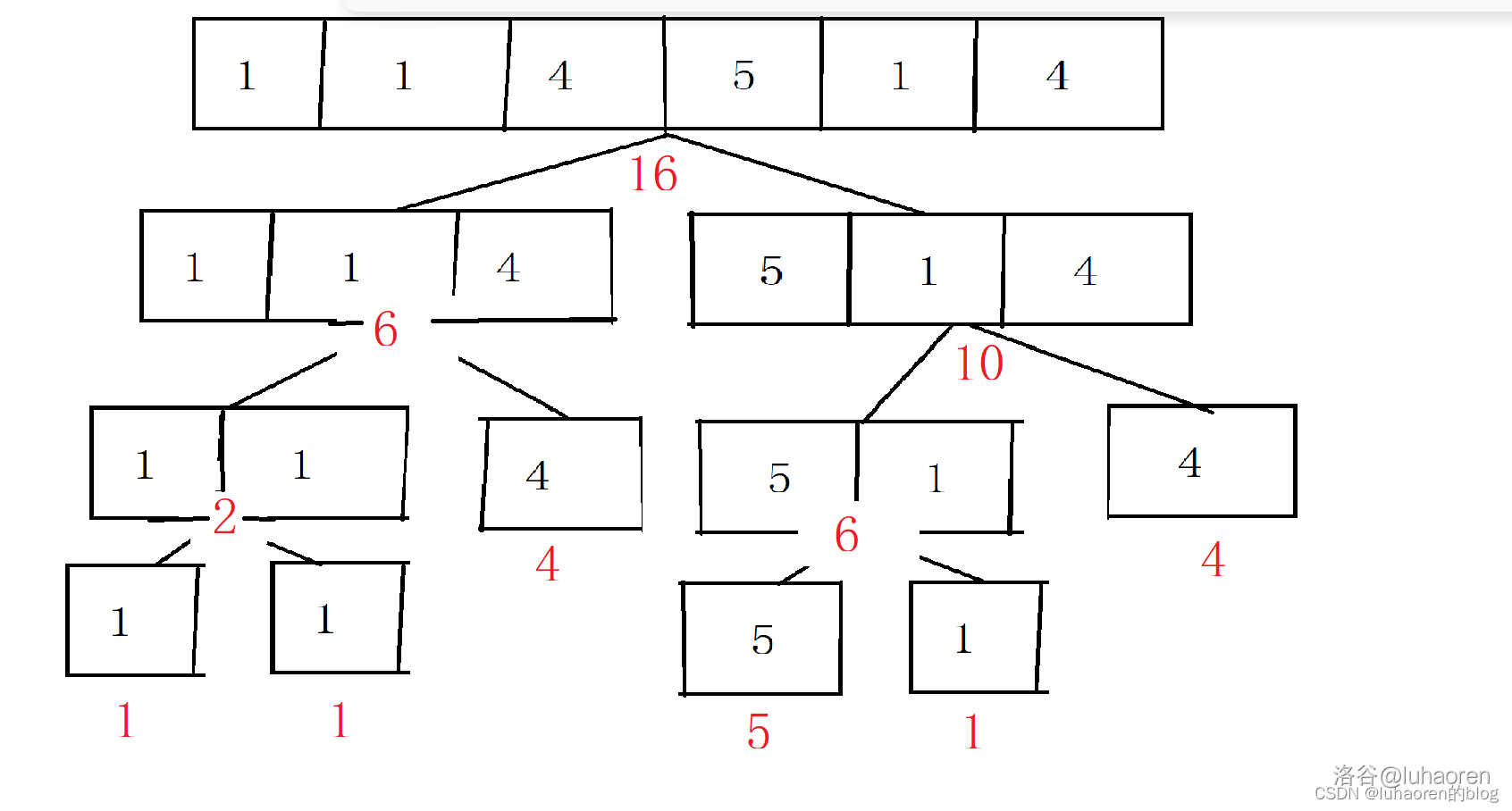
这个建立线段树的过程可以看作是预处理信息，把数组的信息转移到线段树的叶子节点上，时间复杂度大概是 $O(n)$

事实上，还有另一种写法的线段树，不需要建树，但是需要 $O( n\log n)$ 的时间复杂度插入数据，我们会在权值线段树部分介绍这种写法。

建树代码

void build(int x,int l,int r){
	tr[x].l=l,tr[x].r=r;//节点表示区间的左右界
	if(l==r){
		//若l=r，说明这个节点是叶子节点，直接赋值
		tr[x].sum=a[l];//a是原数列
		return;
	}
	int mid=(l+r)/2;//mid表示左右子区间的间隔
	build(x*2,l,mid),build(x*2+1,mid+1,r);//递归建树
	//线段树是完全二叉树，左右子节点可以用x*2,x*2+1表示
	tr[x].sum=tr[x*2].sum+tr[x*2+1].sum;//pushup操作
}

区间查询

线段树可以在 $O(\log n)$ 的时间复杂度下完成区间查询操作。

以刚刚的数列 $\left \{ 1,1,4,5,1,4 \right \}$ 为例。

此时如果询问 $[3,5]$ 之间的区间和，我们该怎么办呢？

首先，如果直接查询 $[4,6]$ 的区间和，我们肯定是会的，直接输出10就行。

查询 $[4,5]$ 怎么办呢？

可以把 $[4,6]$ 拆成 $[4,5]$ 和 $[6,6]$ ，然后输出 $[4,5]$ 的和。

那么 $[3,5]$ 就可以表示为 $[3,3]$ 和 $[4,5]$ 。

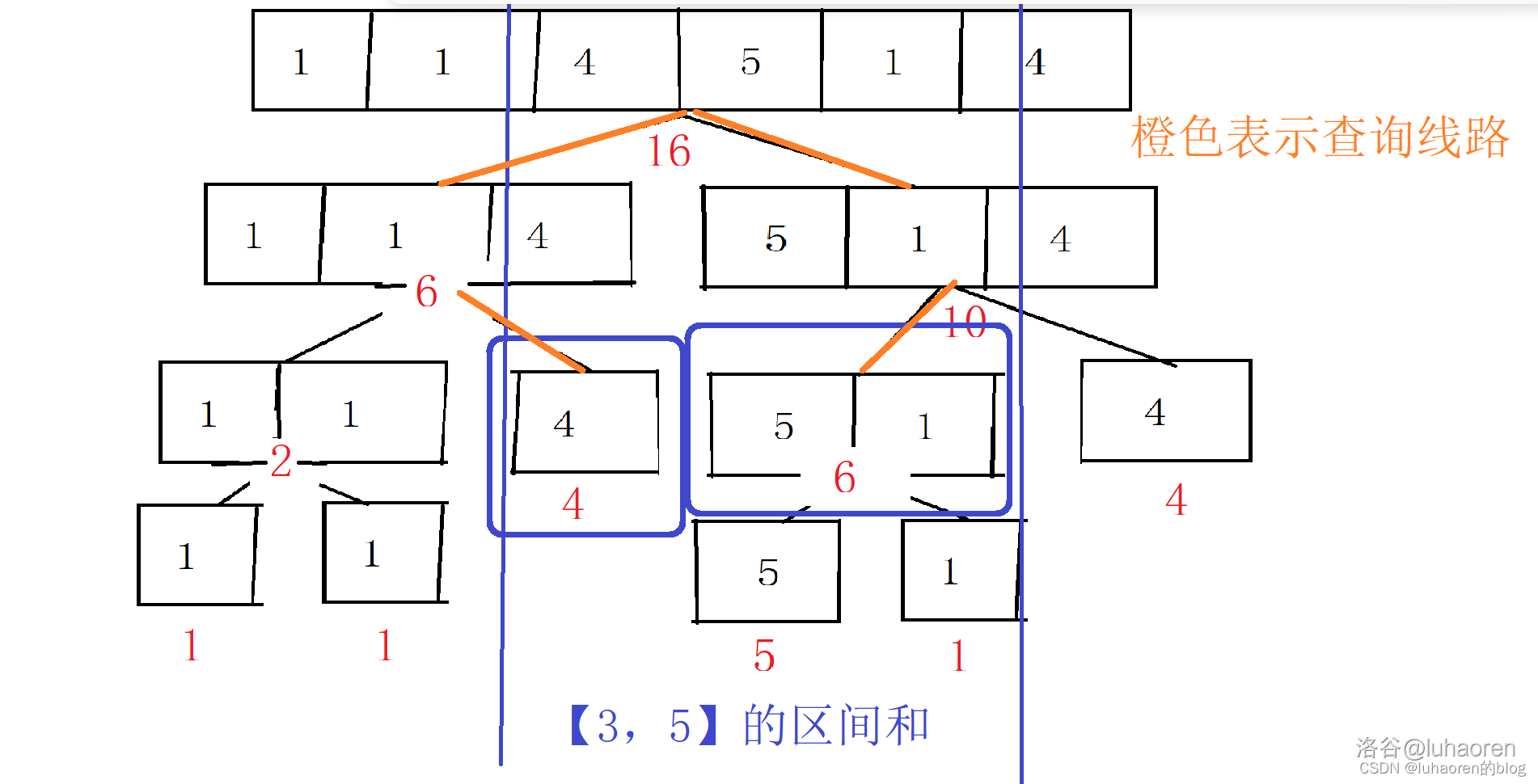
所以无论我们查询多大的区间，都可以拆成一些（不超过 $\log n$ ）预处理过的子区间，把这些子区间的区间和加起来，就是答案。

区间查询代码

int query(int x,int l,int r){
	//区间查询
	if(tr[x].l>=l&&tr[x].r>=r) return tr[x].sum;//如果该节点的区间被要查找的区间包括了，那么就不用继续找了，直接返回改节点的值就行了
	int mid=(tr[x].l+tr[x].r)/2;
	int sum=0;
	if(l<=mid) sum+=query(x*2,l,r);//如果当前节点在要查找区间左边界的右面，那么递归查找左子树
	if(r>mid) sum+=query(x*2+1,l,r);//如果当前节点在要查找区间右边界的左面，那么递归查找右子树
	return sum;//由此得出了该区间的值，返回即可
}

单点修改

单点修改比较简单，不断递归，定位到要找的节点，修改即可。

单点修改

单点修改代码

void change(int now,int x,int k){
	//单点修改
	if(tr[now].l==tr[now].r){
		tr[now].sum=k;//如果找到了该节点，那么修改它
		return;
	}
	int mid=(tr[now].l+tr[now].r)/2;
	if(x<=mid) change(now*2,x,k);//如果要寻找的节点在当前节点的左侧，就递归左子树
	else change(now*2+1,x,k);//否则递归右子树
	tr[now].sum=tr[now*2].sum+tr[now*2+1].sum;//pushup操作，维护每个节点的sum值
}

线段树的存储

观察线段树，我们发现它是一个完全二叉树，可以用堆式储存法。

即把每个节点都存在一个数组里，因为是完全二叉树，所以两个子节点可以用 $2p$ ， $2p+1$ 表示。

因为线段树大部分节点都不是用来存数字的，所以线段树所用的空间要比原数列的空间多很多，如图，只有红色的节点才是真正存数字的。

线段树的存储

线段树大概要开四倍的空间，具体可以看OIwiki上的分析。

例题1：单点修改，区间查询

洛谷P3374

已知一个数列，进行下面两种操作：

将某一个数加上 $x$
求出某区间每一个数的和

题目分析

相当于模板题，可以尝试着敲一遍，这里提供代码。

AC代码

#include <bits/stdc++.h>
using namespace std;
const int N=1e6+10;
struct node{
	int sum,l,r;//线段树节点的结构体
}tr[N*4];//线段树需要开四倍空间
int a[N];
inline void pushup(int x){
	tr[x].sum=tr[x*2].sum+tr[x*2+1].sum;
}
void build(int x,int l,int r){
	tr[x].l=l,tr[x].r=r;//节点表示区间的左右界
	if(l==r){
		//若l=r，说明这个节点是叶子节点，直接赋值
		tr[x].sum=a[l];//a是原数列
		return;
	}
	int mid=(l+r)/2;//mid表示左右子区间的间隔
	build(x*2,l,mid),build(x*2+1,mid+1,r);//递归建树
	//线段树是完全二叉树，左右子节点可以用x*2,x*2+1表示
	pushup(x);//pushup操作
}
int query(int x,int l,int r){
	//区间查询
	if(tr[x].l>=l&&tr[x].r<=r) return tr[x].sum;//如果该节点的区间被要查找的区间包括了，那么就不用继续找了，直接返回改节点的值就行了
	int mid=(tr[x].l+tr[x].r)/2;
	int sum=0;
	if(l<=mid) sum+=query(x*2,l,r);//如果当前节点在要查找区间左边界的右面，那么递归查找左子树
	if(r>mid) sum+=query(x*2+1,l,r);//如果当前节点在要查找区间右边界的左面，那么递归查找右子树
	return sum;//由此得出了该区间的值，返回即可
}
void change(int now,int x,int k){
	//单点修改
	if(tr[now].l==tr[now].r){
		tr[now].sum+=k;//如果找到了该节点，那么修改它
		return;
	}
	int mid=(tr[now].l+tr[now].r)/2;
	if(x<=mid) change(now*2,x,k);//如果要寻找的节点在当前节点的左侧，就递归左子树
	else change(now*2+1,x,k);//否则递归右子树
	pushup(now);//pushup操作，维护每个节点的sum值
}

int n,q;
int main(){
	cin>>n>>q;
	for(int i=1;i<=n;i++) cin>>a[i];
	build(1,1,n);//建树
	while(q--){
		int t,b,c;
		cin>>t>>b>>c;
		if(t==1) change(1,b,c);
		else cout<<query(1,b,c)<<endl;
	}
}

习题

学会了线段树最基础的部分，就可以做一些习题了，将在博客的最后提供题解和代码。

JSOI2008 最大数
线段树维护最大值的模板
loj10123. Balanced Lineup
RMQ问题，可以试试用线段树做

懒标记

下面请思考，怎么才能做到线段树的区间修改呢？

如果直接把区间遍历一遍，依次修改，复杂度会达到无法接受的 $O(n\log n)$ 。

那么怎么能让区间修改的复杂度变小呢？

我们需要引入一个叫做“懒标记”的东西。

懒标记也叫延迟标记，顾名思义，我们再修改这个区间的时候给这个区间打上一个标记，这样就可以做到区间修改的 $O(\log n)$ 的时间复杂度。

如图，如果要给 $[4,6]$ 每个数都加上 $2$ ，那么直接再代表着 $[4,6]$ 区间的结点打上 $+2$ 的标记就行了。

懒标记

pushdown操作

再想一个问题，在给 $[4,6]$ 区间打上懒标记后，我们如何查询 $[4,5]$ 的值？

如果我们直接查询到 $[4,5]$ 区间上，会发现根本就没有被加上过2。

为什么呢?

因为现在懒标记打在了 $[4,6]$ 区间上。而他的子节点压根没被修改过！

所以我们需要把懒标记向下传递。

这就有了一个操作，叫做pushdown，它可以把懒标记下传。

设想一下，如果我们要把懒标记下传，应该注意什么呢？

首先，要给子节点打上懒标记。

然后，我们要修改子节点上的值。

最后，不要忘记把这个节点的懒标记清空。

pushdown代码

inline void pushudown(int x){
	if(tr[x].add){
		//如果这个节点上有懒标记
		tr[2*x].add+=tr[x].add,tr[2*x+1].add+=tr[x].add;
		//把这个节点的懒标记给他的两个子节点
		tr[2*x].sum+=tr[x].add*(tr[2*x].r-tr[2*x].l+1);
		tr[2*x+1].sum+=tr[x].add*(tr[2*x+1].r-tr[2*x+1].l+1);
		//分别给它的两个子节点修改
		tr[x].add=0;
		//别忘了清空这个节点的懒标记
	}
}

区间修改

学会了懒标记，应该可以很轻松地写出区间修改的代码了。

区间修改的操作很像区间查询，也是查找能够覆盖住的子区间，然后给它打上懒标记。

区间查询代码

void update(int now,int l,int r,int k){
	if(l<=tr[now].l&&r>=tr[now].r){
		//如果查到子区间了
		tr[now].sum+=k*(tr[now].r-tr[now].l+1);//先修改这个区间
		tr[now].add+=k;//然后给它打上懒标记
		//注：这里一定要分清顺序，先修改，再标记！
	}
	else{
		//如果需要继续向下查询
		pushudown(now);//一定要先把懒标记向下传
		int mid=(tr[now].l+tr[now].r)/2;
		//这里很像区间查询
		if(l<=mid) update(now*2,l,r,k);
		if(r>mid) update(now*2+1,l,r,k);	
		//最后别忘了pushup一下
		pushup(now);
	}
}

例题2：区间修改，区间查询

洛谷P3372

已知一个数列，你需要进行下面两种操作：

将某区间每一个数加上 $k$ 。
求出某区间每一个数的和。

题目分析

应用到区间修改，需要注意的一点是，在区间查询时，也需要下传懒标记，这样才能查询到真实的值。

AC代码

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
struct node{
	int sum;
	int l,r;
	int add;//懒标记
}tr[N*4];//线段树要开四倍空间哦
int a[N];//原数列
inline void pushup(int x){
	tr[x].sum=tr[2*x].sum+tr[2*x+1].sum;//pushup操作
}
inline void pushudown(int x){
	if(tr[x].add){
		//如果这个节点上有懒标记
		tr[2*x].add+=tr[x].add,tr[2*x+1].add+=tr[x].add;
		//把这个节点的懒标记给他的两个子节点
		tr[2*x].sum+=tr[x].add*(tr[2*x].r-tr[2*x].l+1);
		tr[2*x+1].sum+=tr[x].add*(tr[2*x+1].r-tr[2*x+1].l+1);
		//分别给它的两个子节点修改
		tr[x].add=0;
		//别忘了清空这个节点的懒标记
	}
}
void build(int x,int l,int r){
	//建树操作
	tr[x].l=l,tr[x].r=r,tr[x].add=0;
	if(l==r){
		tr[x].sum=a[l];
		return;
	}
	int mid=(l+r)/2;
	build(2*x,l,mid),build(2*x+1,mid+1,r);
	pushup(x);
}
int query(int x,int l,int r){
	if(l<=tr[x].l&&r>=tr[x].r) return tr[x].sum;
	pushudown(x);//注意，区间查询时也要下懒传标记
	int mid=(tr[x].l+tr[x].r)/2,sum=0;
	if(l<=mid) sum+=query(x*2,l,r);
	if(r>mid) sum+=query(x*2+1,l,r);
	return sum;	
}
void update(int now,int l,int r,int k){
	if(l<=tr[now].l&&r>=tr[now].r){
		//如果查到子区间了
		tr[now].sum+=k*(tr[now].r-tr[now].l+1);//先修改这个区间
		tr[now].add+=k;//然后给它打上懒标记
		//注：这里一定要分清顺序，先修改，再标记！
	}
	else{
		//如果需要继续向下查询
		pushudown(now);//先把懒标记向下传
		int mid=(tr[now].l+tr[now].r)/2;
		//这里很像区间查询
		if(l<=mid) update(now*2,l,r,k);
		if(r>mid) update(now*2+1,l,r,k);
		pushup(now);//最后别忘了pushup一下
	}
}
int n,q;
int main(){
	cin>>n>>q;
	for(int i=1;i<=n;i++) cin>>a[i];
	build(1,1,n);
	while(q--){
		int l,r,k,c;
		cin>>c>>l>>r;
		if(c==1){
			cin>>k;
			update(1,l,r,k);
		}
		else cout<<query(1,l,r)<<endl;
	}
	return 0;
}
//别忘了开long long哦

例题3：较复杂的区间操作

洛谷P3373

已知一个数列，你需要进行下面三种操作：

将某区间每一个数乘上 $x$ 。
将某区间每一个数加上 $x$ 。
求出某区间每一个数的和。

题目分析

有些题要维护多个区间操作，这在pushdown操作上就比较麻烦，比如这道题，要求维护区间加法和区间乘法，所以我们得维护两个懒标记。

那么我们该怎样安排懒标记的pushdown顺序呢？

我们考虑先乘后加的维护顺序，假设两个懒标记分别是 $mul$ 和 $add$ ，那么这个数值就应该是 $mul \times sum+add$ 。

此时如果加上一个 $add$ ，就会变成 $mul \times sum+add+add$

如果乘上一个 $mul$ 那就是 $mul \times sum \times mul+add \times mul$

这种方式便于计算，如果使用先加后乘的方式，就会比较麻烦甚至会出错。

AC代码

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
struct node{
	int l,r;
	int sum,add,mul;
}tr[N*4];//线段树开四倍空间
int a[N];
int n,p,m;
inline void pushup(int x){
	tr[x].sum=(tr[2*x].sum+tr[2*x+1].sum)%p;
}
inline void eval(int x,int add,int mul){
	//我们把计算懒标记单独放在这个函数里，否则好多东西挤一块很难看
	tr[x].sum=(tr[x].sum*mul+add*(tr[x].r-tr[x].l+1))%p;
	tr[x].mul=(mul*tr[x].mul)%p; 	//先计算乘法懒标记
	tr[x].add=(tr[x].add*mul+add)%p;//再算加法懒标记
}

inline void pushdown(int x){
	//依次计算两个子节点的值和懒标记
	eval(x*2,tr[x].add,tr[x].mul);
	eval(x*2+1,tr[x].add,tr[x].mul);
	tr[x].add=0,tr[x].mul=1;
	//清空懒标记，注意：乘法懒标记要初始化成1
}
void build(int x,int l,int r){
	tr[x].l=l,tr[x].r=r;
	tr[x].add=0,tr[x].mul=1;//乘法懒标记要初始化成1
	if(l==r){
		tr[x].sum=a[l];
		return;
	}
	int mid=(l+r)/2;
	build(x*2,l,mid),build(x*2+1,mid+1,r);//递归建树
	pushup(x);
}
void change(int x,int l,int r,int add,int mul){
	if(l<=tr[x].l&&r>=tr[x].r) eval(x,add,mul);//计算
	else{
		pushdown(x);
		int mid=(tr[x].l+tr[x].r)/2;
		if(l<=mid) change(x*2,l,r,add,mul);
		if(r>mid) change(x*2+1,l,r,add,mul);
		pushup(x);
	}
}
int query(int x,int l,int r){
	if(l<=tr[x].l&&r>=tr[x].r) return tr[x].sum;
	int sum=0;
	pushdown(x); //区间查询时也要pushdown  
	int mid=(tr[x].l+tr[x].r)/2;
	if(l<=mid) sum+=query(x*2,l,r)%p;
	if(r>mid) sum+=query(x*2+1,l,r)%p;
	return sum;
}
int main(){
	int t,g,c,ch;
	cin>>n>>m>>p;
	for(int i=1;i<=n;i++) cin>>a[i];
	build(1,1,n);
	while(m--){
		cin>>ch>>t>>g;
		if(ch==1){
			cin>>c;
			change(1,t,g,0,c);          
		}
		else if(ch==2){
			cin>>c;
			change(1,t,g,c,1);          
		}
		else cout<<query(1,t,g)%p<<endl;
	}
	return 0;
}
//记得开longlong

标记永久化

其实，维护区间修改的方式有两种，一种是懒标记和标记下传，另一种叫做”标记永久化“。

标记永久化，就是不下传标记，在每次查询时把经过的标记累加起来，查询时加起来。

标记永久化
如图，打上标记的节点用绿色表示，查询路线（橙色）经过的就累加。

标记永久化代码

const int N=1e4+10;
struct node{
	int sum,add;
	int l,r;
}tr[N*4];
int a[N];
void build(int x,int l,int r){
	tr[x].l=l,tr[x].r=r;
	if(l==r){
		tr[x].sum=a[l],tr[x].add=0;
		return;
	}
	int mid=(l+r)/2;
	build(x*2,l,mid),build(x*2+1,mid+1,r);
	tr[x].sum=tr[x*2].sum+tr[x*2+1].sum;//标记永久化中只有建树时需要用到pushup操作
}
void update(int x,int l,int r,int k){
	tr[x].sum+=(min(tr[x].r,r)-max(tr[x].l,l)+1)*k;//要取一个交集来加
	if(tr[x].l>=l&&tr[x].r<=r){
		tr[x].add+=k;//给节点打上标记后不用下传。
		return;
	}
	int mid=(tr[x].l+tr[x].r)/2;
	if(l<=mid) update(x*2,l,r,k);
	if(r>mid) update(x*2+1,l,r,k);
}
int query(int x,int l,int r,int add){
	if(tr[x].l>=l&&tr[x].r<=r){
		int s=(tr[x].r-tr[x].l+1)*add;//查询到节点后给这个区间乘上add
		return tr[x].sum+s;
	}
	add+=tr[x].add;//add代表查询经过的懒标记之和	
	int mid=(tr[x].l+tr[x].r)/2,sum=0;
	if(l<=mid) sum+=query(x*2,l,r,add);
	if(r>mid) sum+=query(x*2+1,l,r,add);
	return sum;
}