【算法笔记】权值线段树

权值线段树

权值线段树是线段树的一种衍生算法，其基本存储结构和线段树基本相同。

权值线段树

权值线段树与线段树的不同点在于，线段树维护区间信息，权值线段树维护值域信息。

如图，权值线段树就长这个样子。

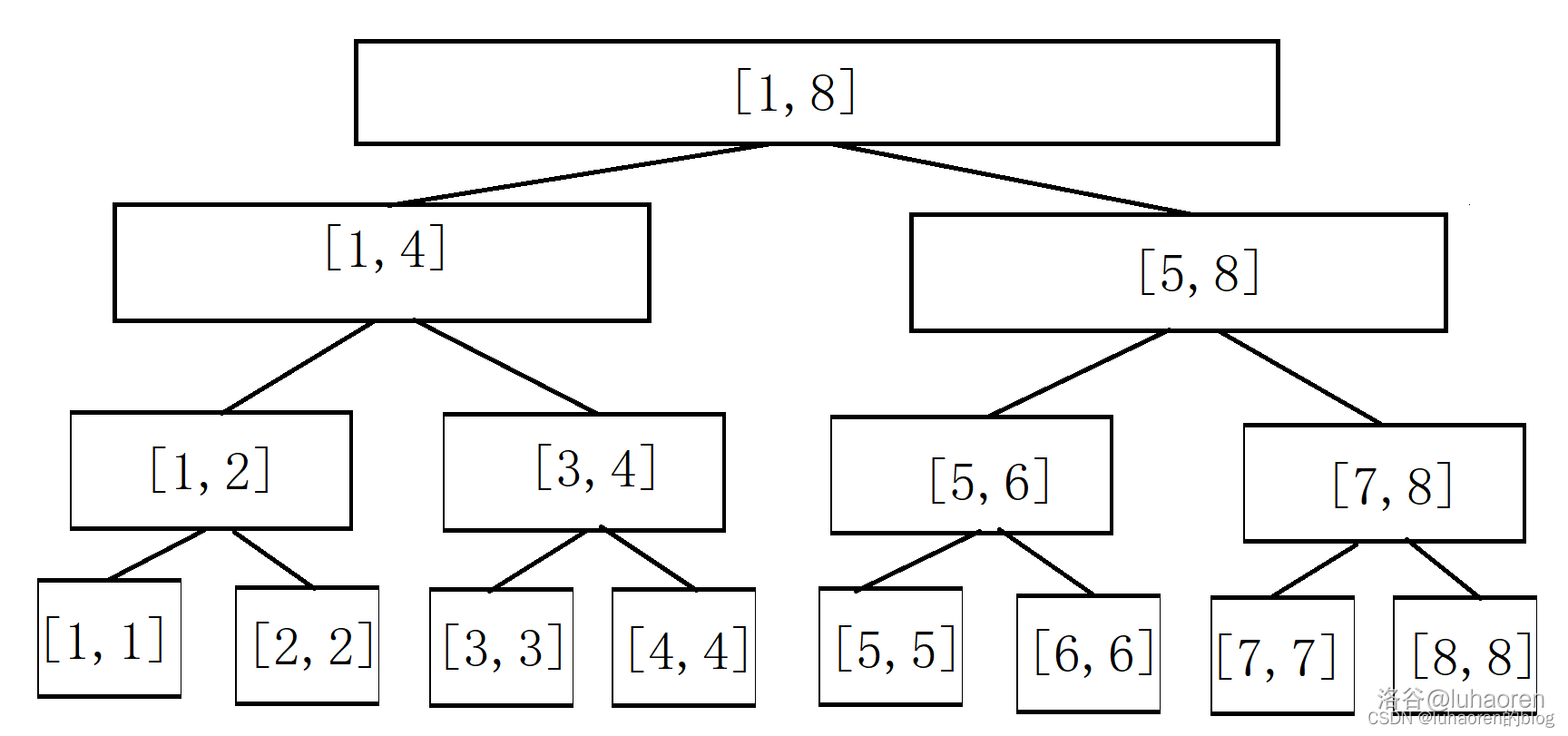
看起来和线段树没什么区别吧，现在我们插入一个数 $4$ 。

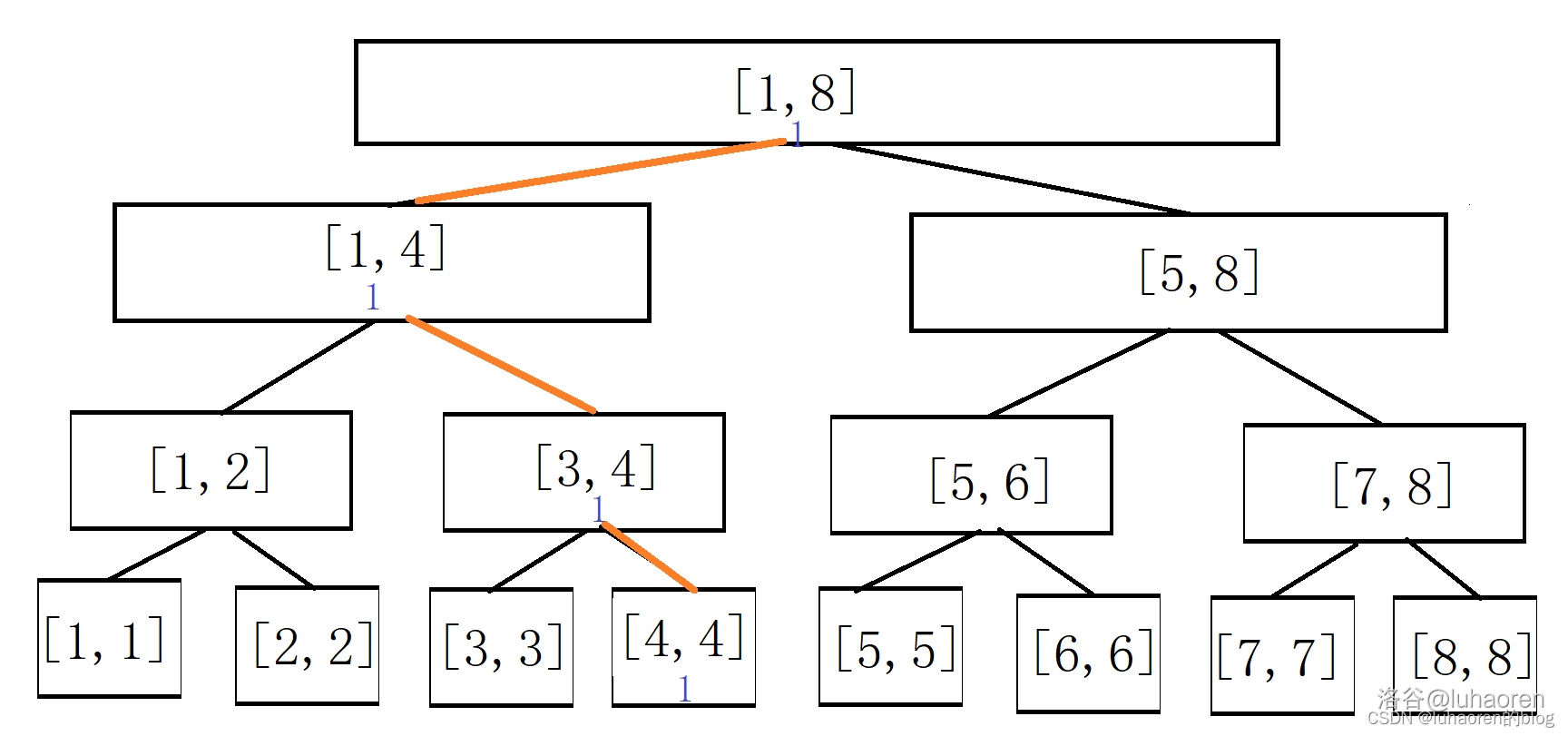
权值线段树插入
每一个包含 $4$ 的区间都被加上了1。

那么每个区间维护的到底是什么呢？

是这个区间内的数的数量。

当我们依次插入 $\{4,1,7,2,8 \}$ 后，这个权值线段树就变成了这样。

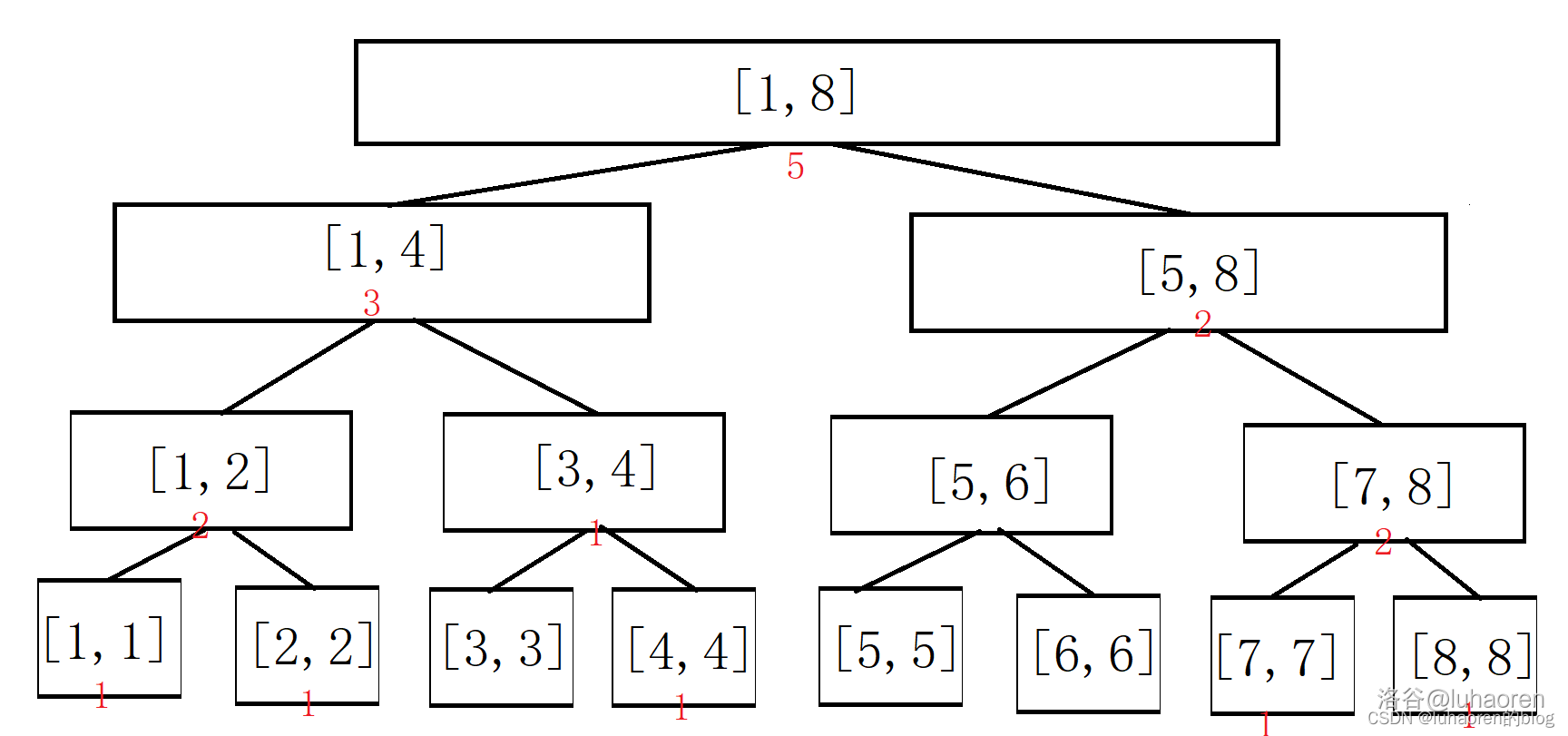
权值线段树插入
这就是权值线段树的原理。

权值线段树可以干很多事情，比如查询第 $k$ 小，查找前驱后继等。

插入与删除

想一想，我们该如何实现插入一个数的操作呢？

把从这个数的节点到根节点的路径上每一个节点都加上1即可。

删除呢？

减去1就行了。

代码模板

int tr[N*4];
//这就是上文提到过的线段树的另一种写法，因为权值线段树不许要维护区间信息，所以不需要建树的预处理，这种写法就变得很方便。
inline void pushup(int x){
	tr[x]=tr[x*2]+tr[x*2+1];
}
void insert(int x,int l,int r,int k){
	//插入一个数k
	if(l==r){
		tr[x]++;
		return;
	}
	int mid=(l+r)/2;
	if(k<=mid) insert(x*2,l,mid,k);
	else insert(x*2+1,mid+1,r,k);
	pushup(x);
}
void del(int x,int l,int r,int k){
	//删除一个数k
	if(l==r){
		tr[x]--;
		return;
	}
	int mid=(l+r)/2;
	if(k<=mid) del(x*2,l,mid,k);
	else del(x*2+1,mid+1,r,k);
	pushup(x);
}
int query(int x,int l,int r,int ql,int qr){
	//查询ql，qr之间一共有多少个数
	if(l>=ql&&r<=qr) return tr[x];
	int mid=(l+r)/2,sum=0;
	if(ql<=mid) sum=query(x*2,l,mid,ql,qr);
	if(qr>mid) sum+=query(x*2+1,mid+1,r,ql,qr);
	return sum;
}

例题4：权值线段树

loj 10116

NK 中学组织同学们去五云山寨参加社会实践活动，按惯例要乘坐火车去。由于 NK 中学的学生很多，在火车开之前必须清点好人数。

初始时，火车上没有学生。当同学们开始上火车时，年级主任从第一节车厢出发走到最后一节车厢，每节车厢随时都有可能有同学上下。年级主任走到第 $m$ 节车厢时，他想知道前 $m$ 节车厢上一共有多少学生。每次提问，m 总会比前一次大。

题目分析

很明显可以用权值线段树做，维护每个区间的数的数量，具体见代码。

AC代码

#include <bits/stdc++.h>
using namespace std;
const int N=5e5+10;
int tr[N*4];//权值线段树维护的是值域，所以要开n的范围的四倍
inline void pushup(int x){
	tr[x]=tr[x*2]+tr[x*2+1];
}
void insert(int x,int l,int r,int k,int p){
	if(l==r){
		tr[x]+=p;
		return;
	}
	int mid=(l+r)/2;
	if(k<=mid) insert(x*2,l,mid,k,p);
	else insert(x*2+1,mid+1,r,k,p);
	pushup(x);
}
int query(int x,int l,int r,int ql,int qr){
	if(l>=ql&&r<=qr) return tr[x];
	int mid=(l+r)/2,sum=0;
	if(ql<=mid) sum=query(x*2,l,mid,ql,qr);
	if(qr>mid) sum+=query(x*2+1,mid+1,r,ql,qr);
	return sum;
}
int n,k;
int main(){
	cin>>n>>k;
	while(k--){
		char opt;
		int m,p;
		cin>>opt;
		if(opt=='A'){
			cin>>m;
			cout<<query(1,1,n,1,m)<<endl;
		}
		else if(opt=='B'){
			//上车
			cin>>m>>p;
			insert(1,1,n,m,p);
		}
		else{
			//下车
			cin>>m>>p;
			insert(1,1,n,m,-p);
		}
	}
}

查询第k大数

请注意，这个查询第k大是针对整个权值线段树的，要查区间第k大请去学主席树或树套树。

权值线段树是维护值域的，一个节点的左右端点都应该是一个具体的数字，而且值域肯定是递增的，所以我们可以二分。

如果 $k$ 小于区间中点，那么也就说明结果为左区间第 $k$ 大数。否则，也就说明结果为右区间第 $k−l_{size}$ 大数。

代码

int kth(int x,int l,int r,int k){
	if(l==r) return l;//查到了，返回即可
	int mid=(l+r)/2;
	if(k<=tr[x*2]) return kth(x*2,l,mid,k); 
	return kth(x*2+1,mid+1,r,k-tr[x*2]);
}

查询一个数的排名

和查询第k大差不多。

每次把 $x$ 与当前区间中点 $mid$ 比较，如果小于等于 $mid$ ，说明在左区间，向左儿子寻找。
如果大于 $mid$ ，说明在右区间，这时，它的排名要加上左子树的大小（它比整个左子树的数都大）

如果找到叶子节点了，那么返回 $1$ (在 $[l,r]$ 的区间只有自己，排名第一)

代码

int rnk(int x,int l,int r,int k){
	if(l==r) return 1;
	int mid=(l+r)/2;
	if(k<=mid) return rnk(x*2,l,mid,k);
	return rnk(x*2+1,mid+1,r,k)+tr[x*2];
}

例题5：用权值线段树实现平衡树

洛谷P3369

实现一个数据结构，来维护一些数，其中需要提供以下操作：

插入 $x$ 数
删除 $x$ 数(若有多个相同的数，应只删除一个)
查询 $x$ 数的排名(排名定义为比当前数小的数的个数 $+1$ )
查询排名为 $x$ 的数
求 $x$ 的前驱(前驱定义为小于 $x$ ，且最大的数)
求 $x$ 的后继(后继定义为大于 $x$ ，且最小的数)

题目分析

正宗解法自然是平衡树，但是仔细观察这些操作，似乎都可以用权值线段树解决？

前四个操作我们已经讲解过了，只剩下最后两个：求前驱和后继。

前驱实际上就是比 $x$ 的排名小一位的数，也就是kth(rnk(x)-1)。

后继就是 $x+1$ 的排名位置的数，也就是kth(rnk(x+1))。

那么我们就可以写出代码了？

没AC代码

#include <bits/stdc++.h>
using namespace std;
const int N=1e7+10;
int tr[8*N];//因为要维护正负区间，所以开二倍，再加线段树的四倍空间，就是八倍
inline void pushup(int x){
	tr[x]=tr[x*2]+tr[x*2+1];
}
void insert(int x,int l,int r,int k,int p){
	//若p为1则插入，若p为-1则删除
	if(l==r){
		tr[x]+=p;
		return;
	}
	int mid=(l+r)/2;
	if(k<=mid) insert(x*2,l,mid,k,p);
	else insert(x*2+1,mid+1,r,k,p);
	pushup(x);
}
int kth(int x,int l,int r,int k){
	//查询排名为k的数
	if(l==r) return l;
	int mid=(l+r)/2;
	if(k<=tr[x*2]) return kth(x*2,l,mid,k); 
	return kth(x*2+1,mid+1,r,k-tr[x*2]);
}
int rnk(int x,int l,int r,int k){
	//查找数k的排名
	if(l==r) return 1;
	int mid=(l+r)/2;
	if(k<=mid) return rnk(x*2,l,mid,k);
	return rnk(x*2+1,mid+1,r,k)+tr[x*2];
}
int n;
int main(){
	cin>>n;
	while(n--){
		int opt,x;
		cin>>opt>>x;
		switch(opt){
		case 1:
			insert(1,-N,N,x,1);//插入
			break;
		case 2:
			insert(1,-N,N,x,-1);//删除
			break;
		case 3:
			cout<<rnk(1,-N,N,x)<<endl;
			break;
		case 4:
			cout<<kth(1,-N,N,x)<<endl;
			break;
		case 5:
			cout<<kth(1,-N,N,rnk(1,0,N,x)-1)<<endl;
			break;
		case 6:
			cout<<kth(1,-N,N,rnk(1,0,N,x)+1)<<endl;
			break;
		}
	}
}

细心的你会发现，这个线段树怎么开了 $8\times10^7$ 呢？肯定会爆空间啊。

但是题目要求的 $|x|\le10^7$ 却令我们不得不开这么大。

怎么办呢？

一般来说，优化线段树空间的有两种方法。

一种是离散化后再进行操作（离线），一种是动态开点。

（这两种方法都会在下一节介绍到）

在这道题中，我们可以使用动态开点的方式，优化空间。

‘动态开点代码

#include <bits/stdc++.h>
using namespace std;
const int N=1e7+10,M=4e5+10;
int tr[M];
int ls[M],rs[M],tot=0;
inline void pushup(int x){
	tr[x]=tr[ls[x]]+tr[rs[x]];//动态开点后，就不能用x*2的方式存了，得开lsrs两个数组（或结构体）
}
void insert(int &x,int l,int r,int k,int p){//x是引用形式，方便传值
	if(!x) x=++tot;//动态开点
	//若p为1则插入，若p为-1则删除
	if(l==r){
		tr[x]+=p;
		return;
	}
	int mid=(l+r)/2;
	if(k<=mid) insert(ls[x],l,mid,k,p);
	else insert(rs[x],mid+1,r,k,p);
	pushup(x);
}
int kth(int x,int l,int r,int k){
	if(l==r) return l;//查到了，返回即可
	int mid=(l+r)/2;
	if(k<=tr[ls[x]]) return kth(ls[x],l,mid,k); 
	return kth(rs[x],mid+1,r,k-tr[ls[x]]);
}
int rnk(int x,int l,int r,int k){
	if(l==r) return 1;
	int mid=(l+r)/2;
	if(k<=mid) return rnk(ls[x],l,mid,k);
	return rnk(rs[x],mid+1,r,k)+tr[ls[x]];
}
int n,root;
int main(){
	cin>>n;
	while(n--){
		int opt,x;
		cin>>opt>>x;
		switch(opt){
		case 1:
			insert(root,-N,N,x,1);//因为动态开点的插入写成引用形式，所以需要带进去一个变量
			break;
		case 2:
			insert(root,-N,N,x,-1);//删除
			break;
		case 3:
			cout<<rnk(root,-N,N,x)<<endl;
			break;
		case 4:
			cout<<kth(root,-N,N,x)<<endl;
			break;
		case 5:
			cout<<kth(root,-N,N,rnk(root,-N,N,x)-1)<<endl;
			break;
		case 6:
			cout<<kth(root,-N,N,rnk(root,-N,N,x+1))<<endl;
			break;
		}
	}
}

如果想学习离散化的解法，可以看这位%%%的博客。

空间优化技巧

这里介绍两种优化方式：离散化和动态开点。

两种方法其实各有优劣，如果只是为了缩小值域，离散化似乎更好写一点，但是动态开点还可以被应用到可持久化、线段树合并和分裂上，所以都学一学吧。

离散化

数据范围太大了，需要缩小数据范围，这句话让你想到了什么？

当然是离散化了！

所以我们可以把所有操作都存起来，排序然后离散化，离线进行操作。

如果你不会离散化，请看这篇博客。

动态开点

动态开点，顾名思义，就是使用的时候再开点。

如果数据范围是 $[-10^7,10^7]$ ，在权值线段树的使用过程中，很大一部分的节点会使用不到，这会造成一种浪费。

动态开点的意思就是：不一上来就把所有的节点全部建立起来，只在需要用到一个节点的时候再建立一个节点。

注意：使用动态开点线段树的话，节点的下标将是无序的，因此必须建立结构体或用两个数组来分别保存一个节点的左右子节点。

代码模板

int tr[M];
int ls[M],rs[M],tot=0;
inline void pushup(int x){
	tr[x]=tr[ls[x]]+tr[rs[x]];//动态开点后，就不能用x*2的方式存了，得开lsrs两个数组（或结构体）
}
void insert(int &x,int l,int r,int k){//x是引用形式，方便传值
	if(!x) x=++tot;//动态开点
	if(l==r){
		tr[x]++;
		return;
	}
	int mid=(l+r)/2;
	if(k<=mid) insert(ls[x],l,mid,k);
	else insert(rs[x],mid+1,r,k);
	pushup(x);
}

习题

提供几道权值线段树的习题。

loj10114.数星星 Stars
权值线段树，需要用动态开点或离散化的优化
P1168 中位数
离散化，然后开权值线段树维护
P2073 送花
可以用权值线段树做
SDOI2014 旅行
树链剖分（如果你会的话），用动态开点维护

#算法笔记 #线段树

【算法笔记】权值线段树

http://luhaoren.xyz/2023/08/12/【算法笔记】权值线段树/

作者

luhaoren

发布于

2023年8月12日

许可协议

【算法笔记】zkw线段树上一篇

【算法笔记】线段树基础下一篇