【算法笔记】可持久化线段树

可持久化线段树

可持久化线段树 ，顾名思义，就是可以保留每一个历史版本，并且支持在历史版本上进行操作的线段树。

可持久化线段树

为什么要可持久化呢?有的时候离线维护扫描线之类的东西时，就需要在时间轴里穿梭，这就需要历史版本；权值线段树如果能可持久化，就可以维护区间的数据，达到静态树套树的效果。

那么如何可持久化呢？

首先，最暴力的做法就是，开$n$个线段树，但是这样肯定会爆空间，所以，我们得想点别的招。

如图，这是一个普通的线段树。

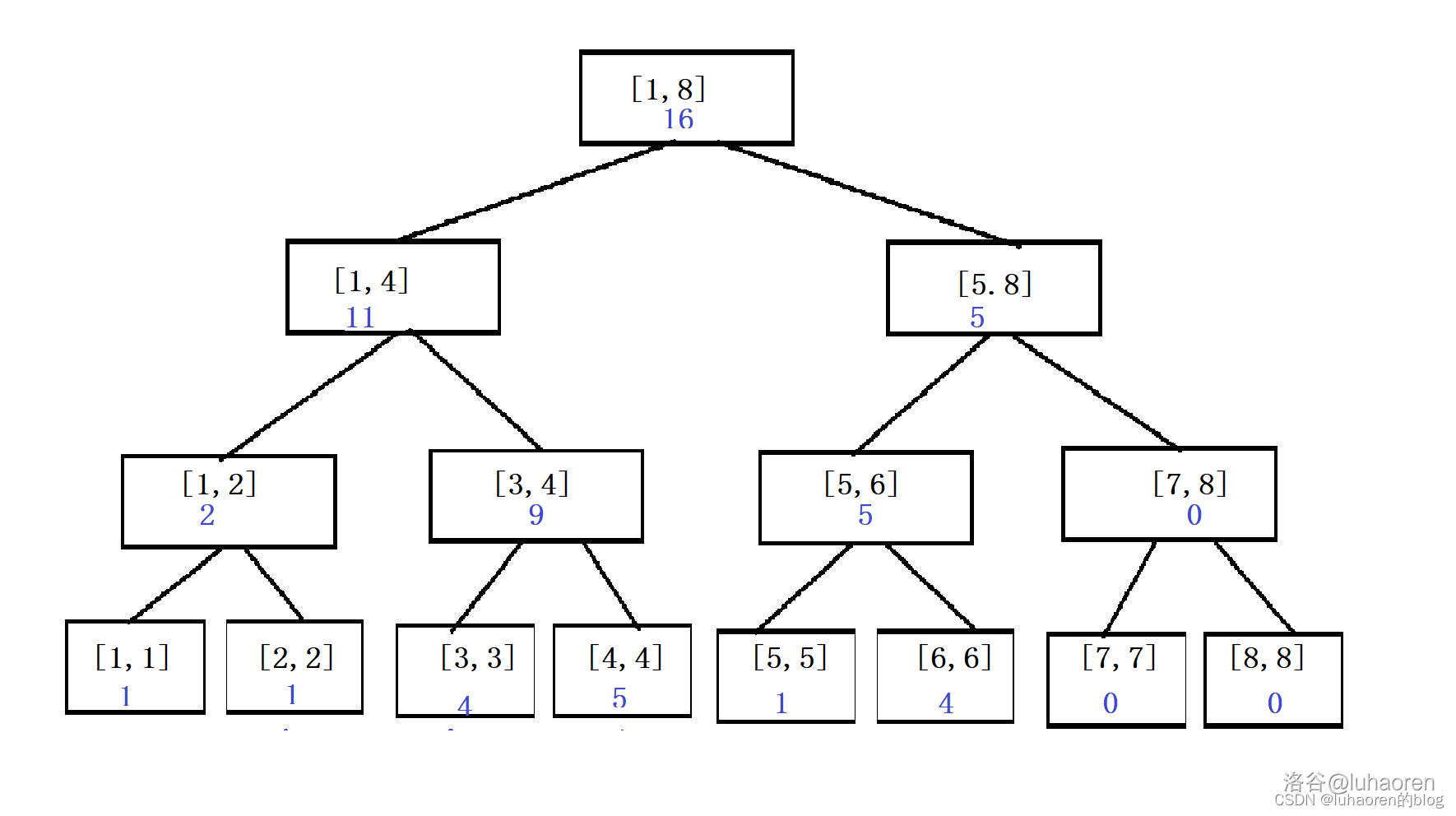
我们把第7个数加上3，如图。

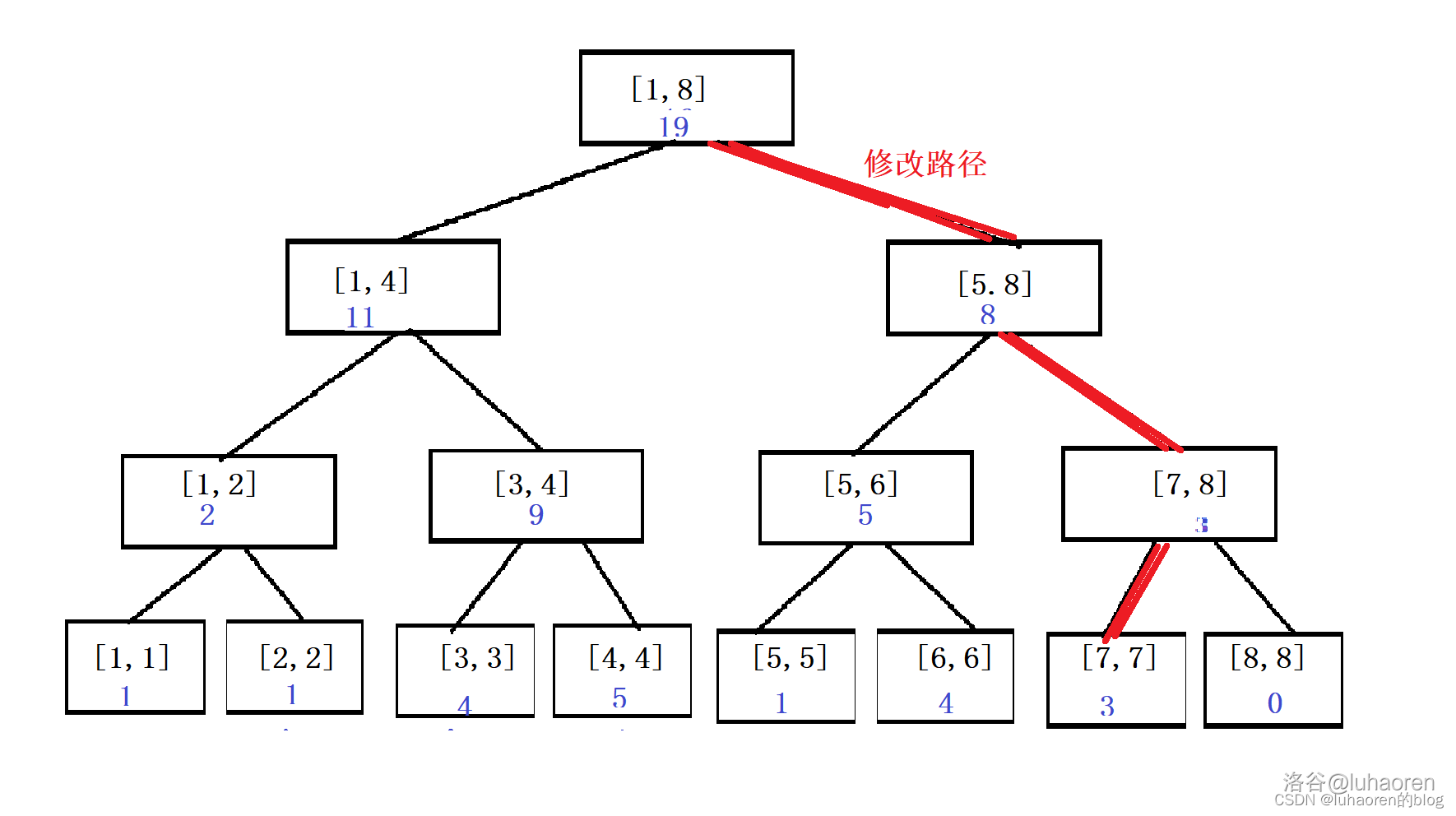
仔细观察，就会发现，被修改的节点实际上只是一条链，长度为$\log n$。

于是，著名神犇hjt突发奇想，如果每次修改只维护一条链的话，空间复杂度就变成$O(n+m\log n)$了呀。

于是就有了可持久化线段树，也叫主席树（能猜到原因吧）

如图，在可持久化线段树里给第7个数加上3。

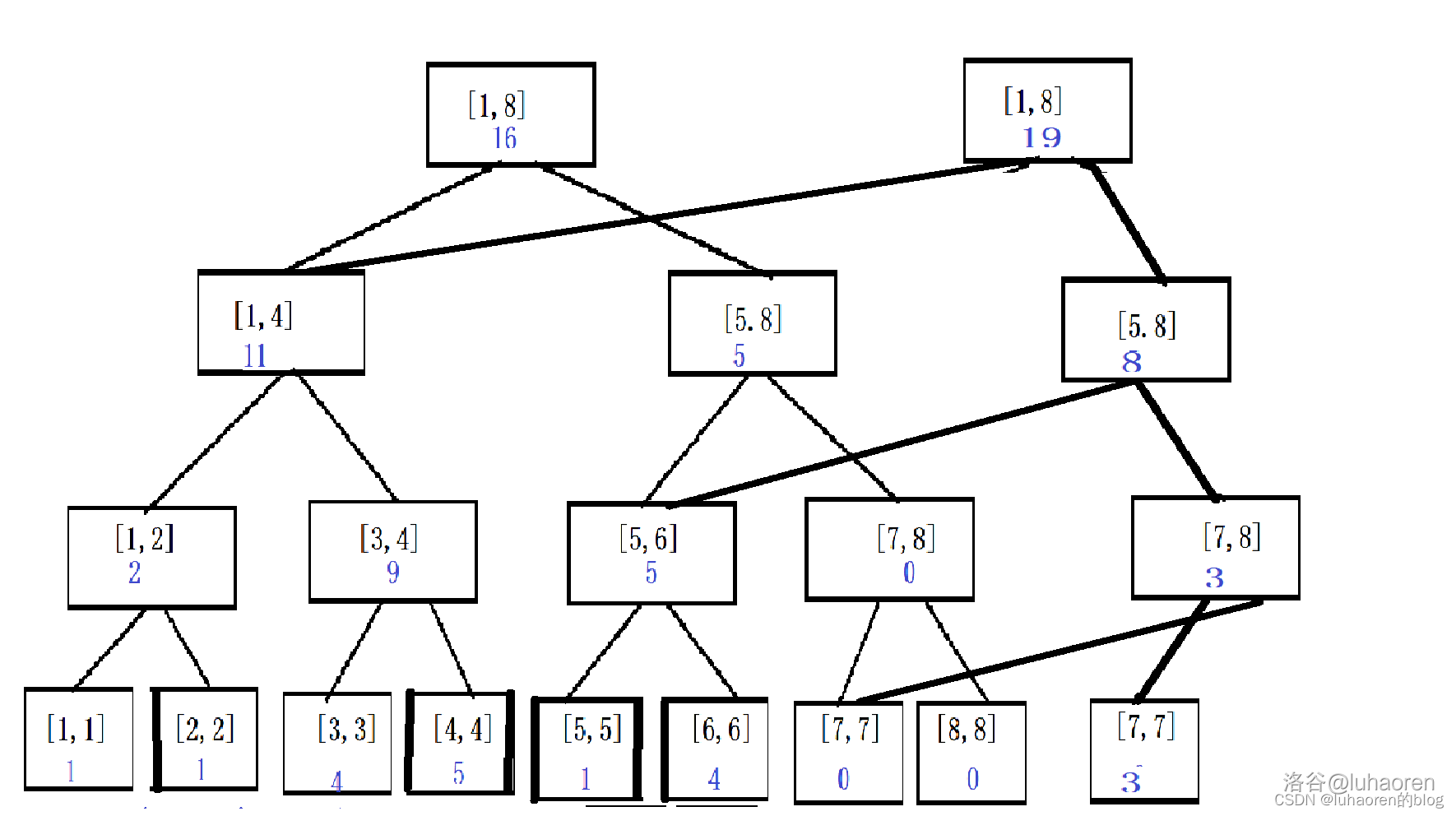
从这个图中，我们可以看出可持久化线段树的诀窍在于——复用历史版本的节点。

可持久化线段树只会增加需要修改的节点，而不需要修改的节点就可以使用以前的结构，这种思想被称为“函数式编程“，所以可持久化线段树也叫”函数式线段树“。

核心代码

void build(int &x,int l,int r){
	//建树操作，即第0个版本，所有版本复用的基础
	x=++tot;//可持久化线段树使用动态开点的方式，因此需要有lsrs数组存储左右儿子节点
	if(l==r){
		tr[x]=a[l];
		return;
	}
	int mid=(l+r)/2;
	build(ls[x],l,mid),build(rs[x],mid+1,r);
	//因为x是引用形式，所以会直接给lsrs数组赋值
}
void change(int u,int &x,int l,int r,int k,int p){
	x=++tot;
	tr[x]=tr[u],ls[x]=ls[u],rs[x]=rs[u];
	//复制原节点
	if(l==r){
		tr[x]=p;
		return;
	}
	int mid=(l+r)/2;
	if(k<=mid) change(ls[u],ls[x],l,mid,k,p);//修改左儿子，右儿子直接复用原节点的右儿子
	else change(rs[u],rs[x],mid+1,r,k,p);//同理
}

例题6：可持久化数组

洛谷P3919

维护这样的一个长度为 $N$ 的数组，支持如下几种操作：

1. 在某个历史版本上修改某一个位置上的值
2. 访问某个历史版本上的某一位置的值

此外，每进行一次操作（对于操作$2$，即为生成一个完全一样的版本，不作任何改动），就会生成一个新的版本。版本编号即为当前操作的编号（从$1$开始编号，版本$0$表示初始状态数组）

题目分析

很明显，这一个可持久化线段树模板题，需要单点修改，单点查询，套用模板即可。

AC代码

#include <bits/stdc++.h>
using namespace std;
const int N=1e6+10,M=5e7+10;//可持久化线段树大概需要O(4n+mlogn)的空间，一般直接开N<<5
int tr[M],root[N],ls[M],rs[M],tot=0,a[N];
void build(int &x,int l,int r){
	x=++tot;
	if(l==r){
		tr[x]=a[l];
		return;
	}
	int mid=(l+r)/2;
	build(ls[x],l,mid),build(rs[x],mid+1,r);
}
void change(int u,int &x,int l,int r,int k,int p){
	x=++tot;//动态开点
	tr[x]=tr[u],ls[x]=ls[u],rs[x]=rs[u];//复制节点
	if(l==r){
		tr[x]=p;
		return;
	}
	int mid=(l+r)/2;
	if(k<=mid) change(ls[u],ls[x],l,mid,k,p);
	else change(rs[u],rs[x],mid+1,r,k,p);
}
int query(int x,int l,int r,int k){
	if(l==r) return tr[x];
	int mid=(l+r)/2;
	if(k<=mid) return query(ls[x],l,mid,k);
	return query(rs[x],mid+1,r,k);
}
int n,m;
int main(){
	scanf("%d%d",&n,&m);//本题稍微有点卡常，需要用printf和scanf
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	build(root[0],1,n);
	for(int i=1;i<=m;i++){
		int v,opt,k,p;
		scanf("%d%d",&v,&opt);
		if(opt==1){
			scanf("%d%d",&k,&p);
			change(root[v],root[i],1,n,k,p);
		}
		else{
			scanf("%d",&k);
			printf("%d\n",query(root[v],1,n,k));
			root[i]=root[v];
		}
	}
}

例题7：静态区间第k小

洛谷P3834

给定$n$ 个整数构成的序列 $a$，将对于指定的闭区间 $[l,r]$ 查询其区间内的第 $k$ 小值。

题目分析

如果没有区间操作，查询第k小可以用权值线段树实现，如果有要支持区间操作呢？

我们建一颗可持久化权值线段树，如图，把$\{2,4,1,3\}$这个数列的数依次插入。

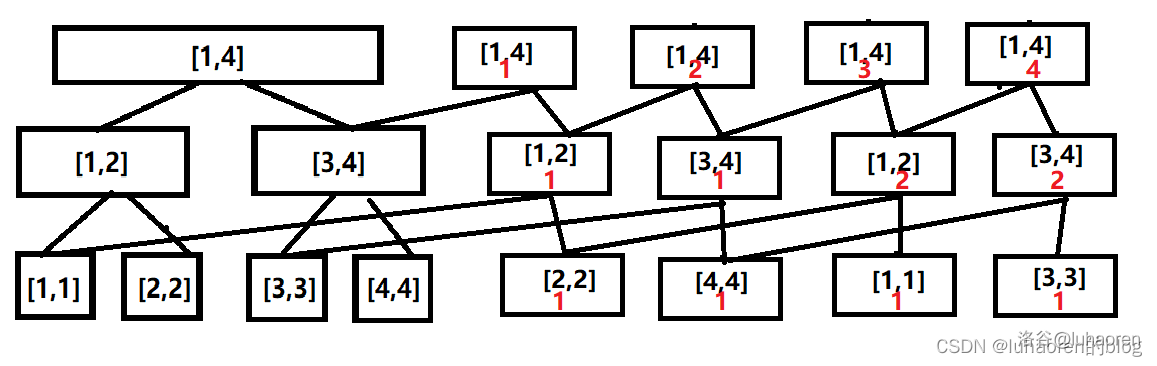
仔细观察，就会发现第$i$棵树保存着前$i$个数的信息（设初始化的树为第$0$棵）

也就是说，这个可持久化线段树可以说是数列的“前缀树”。

你能想到什么？

可持久化线段树满足区间可加减性，所以我们可以用前缀和的方式找出维护$[l,r]$个数的信息的树。

也就是拿出第$l-1$棵树和第$r$棵树，两者相减，结果就是$[l,r]$的信息。

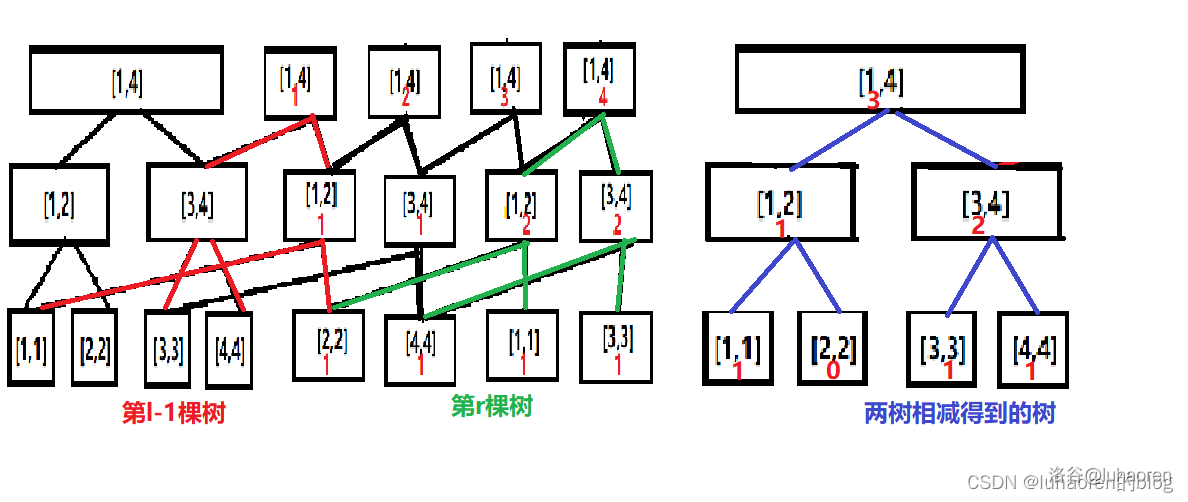
而在相减后的树上找第k小相信大家都已经会了。

那么就可以写出代码了！

注：这题数据很水，题面给$|a_i |\le 10^9$，但实际上的数据范围是$0 \le a_i \le 10^6$，甚至不需要离散化的优化，就可以过。

AC代码

#include <bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int tr[N<<5],ls[N<<5],rs[N<<5],root[N],tot=0;
void build(int &x,int l,int r){
    //建树
	x=++tot;
	if(l==r) return;
	int mid=(l+r)/2;
	build(ls[x],l,mid),build(rs[x],mid+1,r);
}
void insert(int u,int &x,int l,int r,int k){
	x=++tot;//动态开点
	tr[x]=tr[u]+1,ls[x]=ls[u],rs[x]=rs[u];//复制该节点的所有信息（可以直接在节点上+1，否则还得pushuo一遍）
	if(l==r)  return; 
	int mid=(l+r)/2;
	if(k<=mid) insert(ls[u],ls[x],l,mid,k);
	else insert(rs[u],rs[x],mid+1,r,k);
}
int query(int u,int v,int l,int r,int k){
	int mid=(l+r)/2,lx=tr[ls[v]]-tr[ls[u]];//两颗树信息相减得到的左儿子信息
	if(l==r) return l;//如果只有一个数，第几大都是这个数了，直接返回
	if(k<=lx) return query(ls[u],ls[v],l,mid,k);
	return query(rs[u],rs[v],mid+1,r,k-lx);//二分查找第k小
}
int n,m;
int main(){
	cin>>n>>m;
	build(root[0],0,1e6);//建树
	for(int i=1;i<=n;i++){
		int t;
		cin>>t;
		insert(root[i-1],root[i],0,1e6,t);
	}
	while(m--){
		int l,r,k;
		cin>>l>>r>>k;
		cout<<query(root[l-1],root[r],0,1e6,k)<<endl;
	}
}

实际上，这份代码在除了洛谷以外的其它OJ上是AC不了的，因为题面上$|a_i|\le 10^9$的数据范围使代码必须要有离散化的优化，这里给出优化代码。

//其他部分和前面无异，这以后是离散化代码
int n,m,tt=0;
map<int,int>mp;//使用map离散化，使用sort离散化也可以
int val[N],a[N];
int main(){
    cin>>n>>m;
    build(root[0],1,n);
    for(int i=1;i<=n;i++){
        cin>>a[i];
        mp[a[i]]=0;
    }
    for(auto &it:mp){
    //map会自己排序，在遍历的过程中标上映射后的序号
        it.second=++tt;
        val[tt]=it.first;
    }
    for(int i=1;i<=n;i++) insert(root[i-1],root[i],1,n,mp[a[i]]);
    while(m--){
        int l,r,k;
        cin>>l>>r>>k;
        cout<<val[query(root[l-1],root[r],1,n,k)]<<endl;
    }
}

习题

1. 洛谷P3402 可持久化并查集
   注意并查集的合并操作
2. [POI2014] KUR-Couriers
   维护区间绝对众数，有乱搞做法