【算法笔记】模拟退火

模拟退火的引入

假如我们有一个函数，要求它的极大值，怎么求呢？

如果这个函数满足单调性，可以用二分的方法。

如果这是一个单谷（或单峰）函数，可以用三分法。

那要是多峰函数怎么半呢？

这时就可以用随机化算法。

一种朴素的方法是：每次在当前找到的最优方案 $x$ 附近寻找一个新方案。如果这个新的解 $x'$ 更优，那么转移到 $x'$ ，否则就不转移。（这被称作爬山算法）

但是这样就容易陷入一种局部最优解，如图，如果使用爬山算法，找到的答案可能在一个范围内是最优解，但是在全局上并不是最优解。
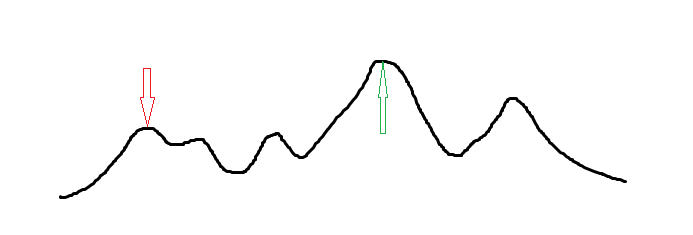
图片来自oiwiki
所以就有了模拟退火算法。

模拟退火算法的基本思路是，在一定的概率下接受一个非最优解而跳出局部最优解。
百年老图

为什么这个算法被称为模拟退火呢？因为物理中金属降温是随机的，这个金属降温的过程也叫退火。

基本概念

刚刚讲到了模拟退火接受非最优解的概率，这个概率被称为 $Metropolis$ 准则，也就是

e^{\frac{-\Delta E}{T}}

其中， $\Delta E$ 表示最优解和当前解的差， $T$ 是当前温度。

模拟退火一般有三个参数，初始温度 $T_0$ ，降温系数 $\Delta T$ （一般取 $0.99$ 左右），最终温度 $T_{last}$ （一般是个极小值）。

当前温度 $T$ 从 $T_0$ 开始，不断乘以 $\Delta T$ ，在这个过程中不断接受新解，直到 $T$ 降至 $T_{last}$ ，算法结束。

模板

这里以UVA10228（费马点问题）为例。

#include <bits/stdc++.h>
using namespace std;
const double eps=1e-8;
struct xy{double x,y;};
int n;
xy point[1010],anst,now;
double ans;
double calc(xy k){
    //计算当前解距各点的距离
	double ans=0;
	for(int i=1;i<=n;i++)  ans+=sqrt((point[i].x-k.x)*(point[i].x-k.x)+(point[i].y-k.y)*(point[i].y-k.y));
	return ans;
}
void sa(){
	for(double t=3000;t>eps;t*=0.999){
		//降温过程
		double cx=now.x+(rand()*2-RAND_MAX)*t;
		double cy=now.y+(rand()*2-RAND_MAX)*t;//随机出新解
		double k=calc({cx,cy});//计算新解
		double da=k-ans;//计算新解与最优解的差
		if(da<0){
		    //如果新解比最优解还好，直接接受
			now=anst={cx,cy};
			ans=k;
		}
		else if(exp(-da/t)*RAND_MAX>rand()) now={cx,cy};//否则根据概率接受
	}
}
int main(){
	srand(19260817);//随机种子
	int t;
	cin>>t;
	while(t--){
    	cin>>n;
    	for(int i=1;i<=n;i++){
    		cin>>point[i].x>>point[i].y;
    		anst.x+=point[i].x,anst.y+=point[i].y;
    	}
    	anst.x/=(double)n,anst.y/=(double)n;
    	ans=calc(anst);//初始解（所有坐标的平均值）
    	for(int i=1;i<=100;i++) sa();//跑模拟退火
    	printf("%.0lf\n",calc(anst));//输出解
    	if(t) cout<<endl;
	}
	return 0;
}

应用

在OI中，模拟退火一般有三种用途，一种是计算几何（比如费马点问题），一种是序
列问题（随机交换），还有一种是骗分。

这篇博客的最后会有几道例题，并附讲解。

技巧

模拟退火本质上是一种随机化算法，能否正确取决于参数和rp。

这里提供几种技巧，在考试时可以使用。

卡时技巧

一般来说，模拟退火要跑很多遍才能跑出最优解，但是没遍模拟退火的时间我们也不知道，所以可以用 $clock$ 函数，判断剩余时间，来卡时。

1	`while((double)clock()/CLOCKS_PER_SEC<0.8) sa();`

注：clock函数返回从程序开始到当前的时间，CLOCKS_PER_SEC将clock()函数的结果转化为以秒为单位的量，每个系统都不一样，在windows系统里是1000。

参数调小

一般来说，参数过大会WA，参数过小会TLE。

但是TLE的可能性一般比WA小，所以调参时宁小毋大，如平衡点一题，如果参数设置为 $10^{-8}$ ，只能得到十分，如果设为 $10^{-14}$ ，就能得到满分。

坐标的随机

在费马点问题中，假如当前坐标是 $x,y$ ，如果随机到下一个坐标？

如果这么些：

1	`double cx=x+rand(),cy=y+rand();`

rand的取值是一个正值，所以坐标会逐渐递增，这显然是不行的。

所以我们可以这样写：

1 2	`double cx=now.x+(rand()2-RAND_MAX)t; double cy=now.y+(rand()2-RAND_MAX)t;`

RAND_MAX是随机数的最大值，所以(rand()*2-RAND_MAX)的取值范围就是[-RAND_MAX,RAND_MAX]，再乘上当前的温度 $t$ ，就会得到一个可能正负的随机浮点数，并且随着温度的减小越来越小，满足了我们的需求。

例题

P1337 平衡点 / 吊打XXX

原题

这题需要一定的物理知识。

根据能量最低原理，一个系统内能量越低就越稳定，所以题目要求的平衡情况能量肯定最小。

分析这道题，如果静止不动，则能量只有重力势能，所以直接令重力势能最小即可。

我们知道，重力势能的公式是

E_p=mgh

$g$ 是个常量，所以直接算每个点的质量和高度乘积即可。

简化题意后，就是寻找一个点，让这个点到每个点的距离乘以质量最小，也就是一个带权费马点问题，套用模板即可。

AC代码

#include <bits/stdc++.h>
using namespace std;
const double eps=1e-15;
struct xy{double x,y;};
int n;
xy point[1010],anst,now;
double w[1010];
double ans;
inline double calc(xy k){
	double ans=0;
	for(int i=1;i<=n;i++)  ans+=w[i]*sqrt((point[i].x-k.x)*(point[i].x-k.x)+(point[i].y-k.y)*(point[i].y-k.y));
	return ans;
}
void sa(){
    for(double t=3000;t>eps;t*=0.999){
		double cx=now.x+(rand()*2-RAND_MAX)*t;
		double cy=now.y+(rand()*2-RAND_MAX)*t;//随机出新解
		double k=calc({cx,cy});//比较新解和最优解
		double da=k-ans;//计算差值
		if(da<0){
		    //如果新解比最优解好，直接接受
			now=anst={cx,cy};
			ans=k;
		}
		else if(exp(-da/t)*RAND_MAX>rand()) now={cx,cy};//否则按照概率接受
	}
}
int main(){
	srand(19260817);
	cin>>n;
	for(int i=1;i<=n;i++){
	    cin>>point[i].x>>point[i].y>>w[i];
	    anst.x+=point[i].x,anst.y+=point[i].y;
	}
	anst.x/=(double)n,anst.y/=(double)n;
	ans=calc(anst);
	while((double)clock()/CLOCKS_PER_SEC<0.8) sa();//卡时
	printf("%.3lf %.3lf",anst.x,anst.y);
}

P5544 炸弹攻击1

原题

大意是找到一个点，以它为圆心的圆能覆盖最多的点。

这题的关键是计算，首先这个半径不能超过 $r$ ，其次这个圆不能与别的圆重合，找到符合这两个条件的最小的圆，计算它覆盖的点即可。

其它的部分套就是个费马点问题了，套模板即可

AC代码

#include <bits/stdc++.h>
using namespace std;
struct build{
    double x,y,r;
}b[20];
struct xy{
    double x,y;
}a[1010],ans;
double n,m,r,ansn=1e8;
inline double dis(xy a,xy b){
    return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
int calc(xy k){
	double minn=r,ans=0;
	for(int i=1;i<=n;i++) minn=min(minn,dis(k,{b[i].x,b[i].y})-b[i].r);
	for(int i=1;i<=m;i++) if(dis(k,a[i])<=minn) ans++;
	return ans;
}
void sa(){
	for(double T=3000;T>1e-16;T*=0.99){
		double cx=ans.x+(rand()*2-RAND_MAX)*T,cy=ans.y+(rand()*2-RAND_MAX)*T;
		double da=calc({cx,cy})-ansn;
		if(da>0){
			ans.x=cx,ans.y=cy;
			ansn=calc({cx,cy});
		}
		else if(exp(da/T)>rand()) ans={cx,cy};
	}
}
int main(){
	srand(19260817);
	cin>>n>>m>>r;
	for(int i=1;i<=n;i++) cin>>b[i].x>>b[i].y>>b[i].r;
	for(int i=1;i<=m;i++){
		cin>>a[i].x>>a[i].y;
		ans.x+=a[i].x,ans.y+=a[i].y;
	}
	ans.x/=m,ans.y/=m,ansn=calc(ans);
	for(int i=1;i<=100;i++) sa();
	cout<<ansn;
	return 0;
}

P3878 分金币

以这道题为例，我们介绍一种模拟退火的其它应用。

本题大意是把 $n$ 个数分成两半，让它们的和的差值最小。

模拟退火可以解决这种序列问题，以随机概率交换两个数，计算当前的差值，如果更优，就接受，否则以一定概率接受（如果不接受就把它们换回去）

AC代码

#include <bits/stdc++.h>
using namespace std;
const double q=0.999,eps=1e-14;
int n,a[60],ans=1e9;
int calc(){
	int s1=0,s2=0;
	for(int i=1;i<=(n+1)/2;i++) s1+=a[i];
	for(int i=(n+1)/2+1;i<=n;i++) s2+=a[i];
	return abs(s1-s2);
}
void sa(){
    for(double T=5000;T>eps;T*=q){
		int l=rand()%n+1,r=rand()%n+1;//取数列中随机两个数
		swap(a[l],a[r]);//交换它们
		int da=ans-calc();
		if(da>0) ans-=da;
		else if(exp(da/T)*RAND_MAX<rand()) swap(a[l],a[r]);
		//这个意思是，如果不满足那个概率，就给他回复原状
	}
}
int main(){
	srand(19260817);
	int t;
	cin>>t;
	while(t--){
		ans=1e9;
		cin>>n;
		for(int i=1;i<=n;i++) cin>>a[i];
		for(int i=1;i<=20;i++) sa();
		cout<<ans<<endl;
	}
}

练习题

P4703 偷上网
P2538 城堡
P4035 球形空间产生器

#算法笔记 #模拟退火

【算法笔记】模拟退火

http://luhaoren.xyz/2023/08/01/【算法笔记】模拟退火/

作者

luhaoren

发布于

2023年8月1日

许可协议

OI程序优化指南上一篇

【算法笔记】FHQtreap 下一篇