【算法笔记】FHQtreap
前言
FHQtreap绝对是平衡树里最好写,最实用的,他几乎能做所有splay或其它平衡树能做的事,还能可持久化!
这篇文章将会介绍FHQtreap的基本操作和维护区间的操作,并附上例题。
基本操作
FHQtreap的基本操作只有两个,分裂和合并。
有些读者可能会问,分裂和合并和平衡树有什么关系?
想想一下,如果要插入一个数3,在正常的平衡树里应该是找到3的位置,然后让他的值,在FHQtreap里可不是这样,所谓插入,就是把平衡树按照3分裂成两棵树,然后把3这个数的节点合并进去。
删除呢?直接按照3分裂,然后在左子树里把3“抠出去”,再合并。
其它操作也大同小异,你会发现,大部分平衡树的操作,都可以用分裂和合并来表示,这就是FHQtreap的特点,这种思想被称为“函数式编程”。
节点结构
FHQtreap每个节点要保存的信息有权值(这个数),优先级(随机数),子树大小,左右子树的编号。
1 | |
注意:FHQtreap不需要存储,它把权值相同的节点看成多个节点 。
pushup操作
也叫maintain 操作,调整子树大小。
1 | |
分裂
FHQtreap的分裂操作有两种,一种是通过权值分裂(小于等于的分到左子树,大于的分到右子树),一种是通过大小分裂(前个数分到左子树,剩下的分到右子树)
如图,将一棵树按7分裂成两棵树。
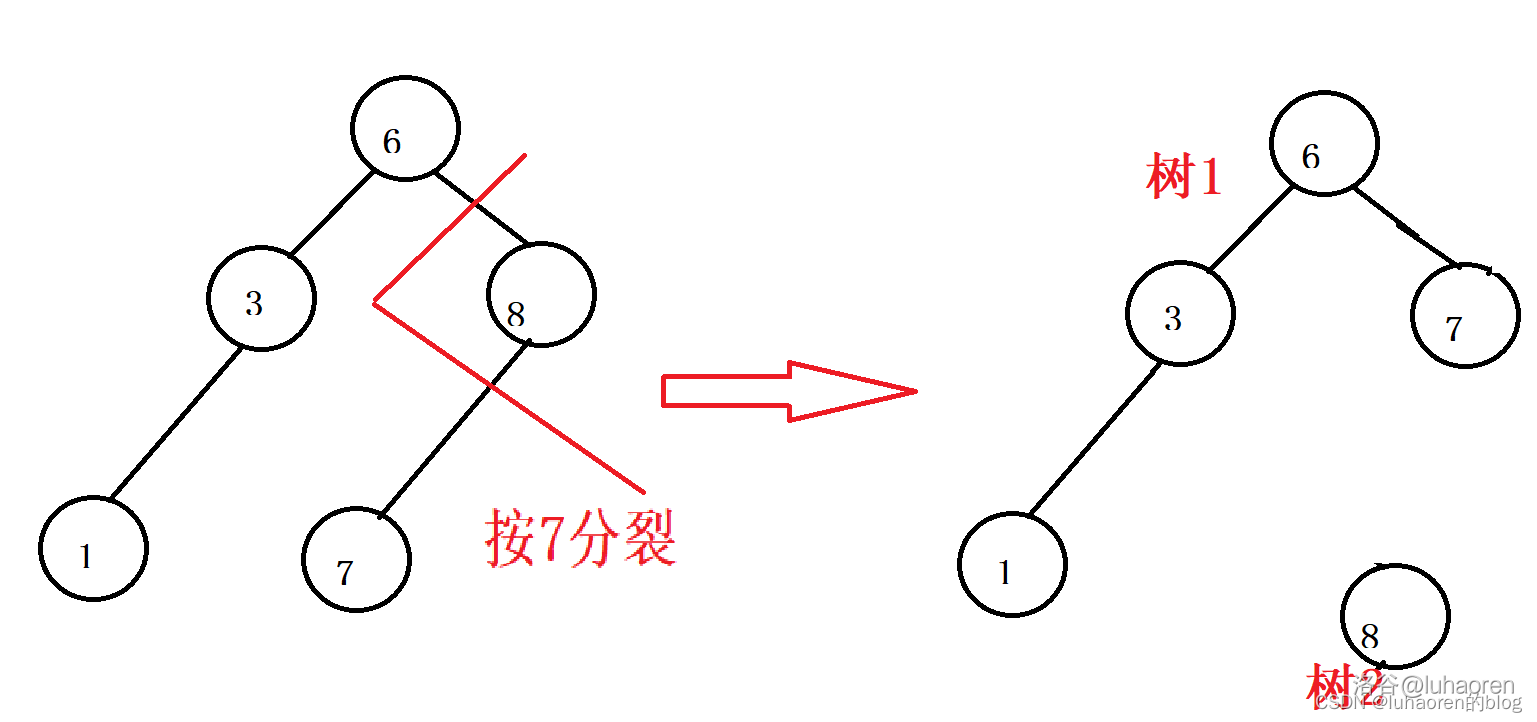
分裂后,就产生了和两颗树。
按权值分裂代码
1 | |
FHQtreap也可以按照大小分裂,将在区间操作的部分提到,这里给出代码。
按大小分裂代码
1 | |
合并
FHQtreap的合并操作很像是线段树合并,是一种启发式合并。
如图,合并操作可以有多种合并方式,这取决于每个节点所附带的优先级(随机值),使这颗树的优先级符合性质(感兴趣的可以了解一下treap的平衡方式,这里不细讲了)
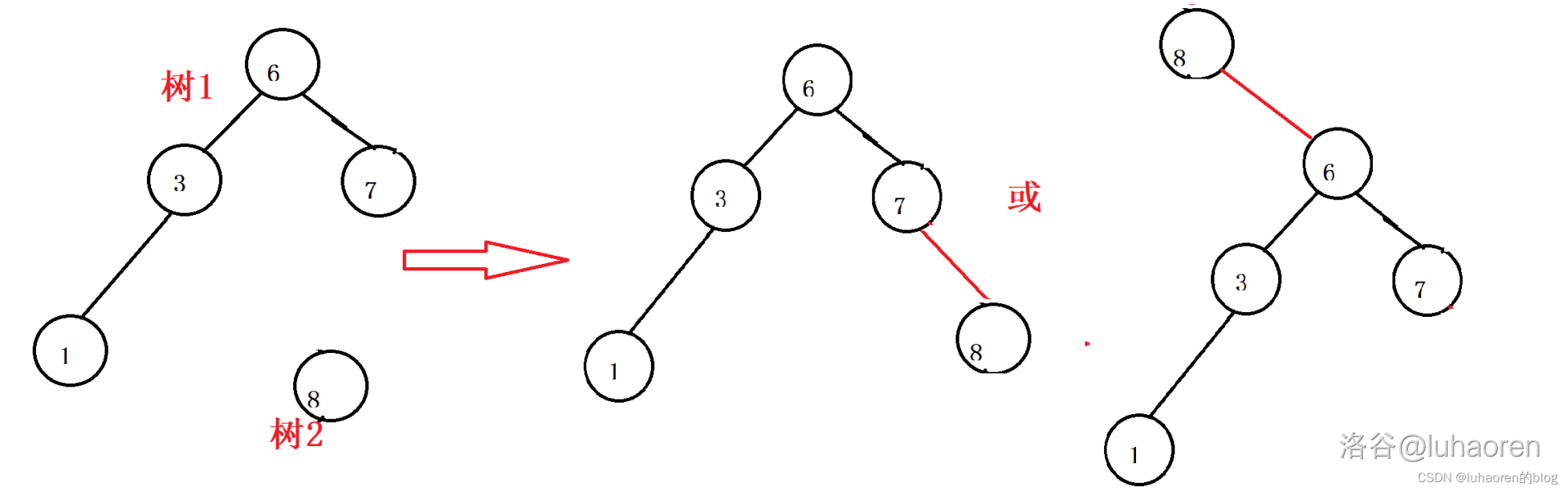
合并操作代码
1 | |
其它操作
学会了基本的分裂和合并操作,我们就可以做到插入,删除这些操作了。
新建节点
这个新建节点的操作大概是本人独有的,大部分oier都不会这么写,但是这么写的好处就是简短清晰(只需两行)。
1 | |
插入
如图,若插入一个,先按分裂,然后新建一个节点合并进去。
插入代码
1 | |
删除
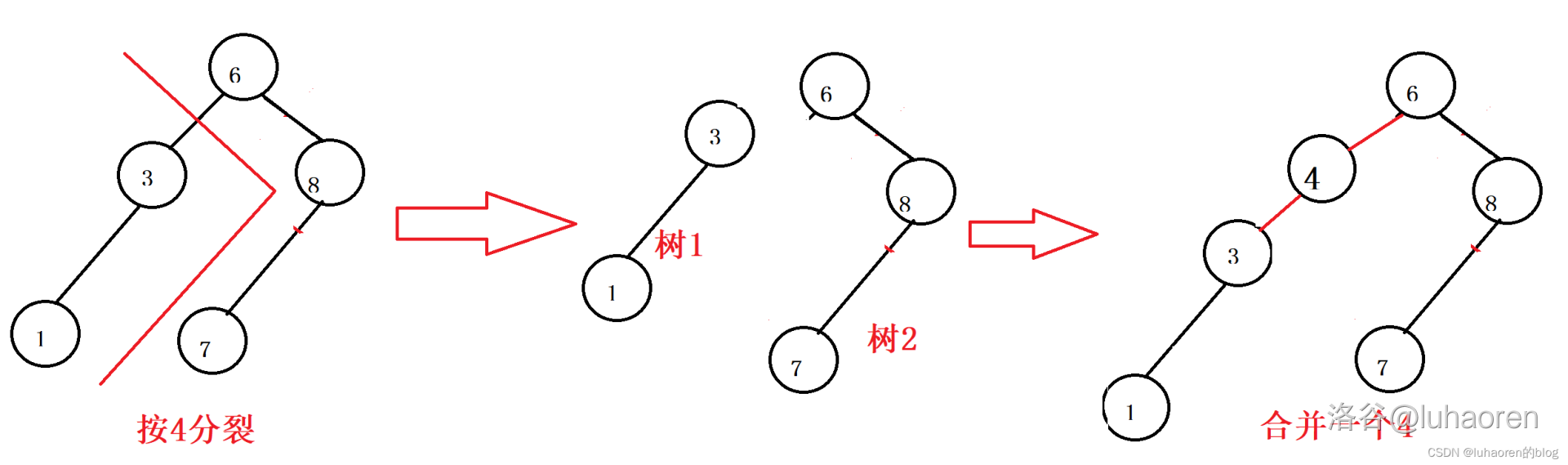
删除操作比较复杂,如图,先按分裂成两颗子树(树1和树2)。
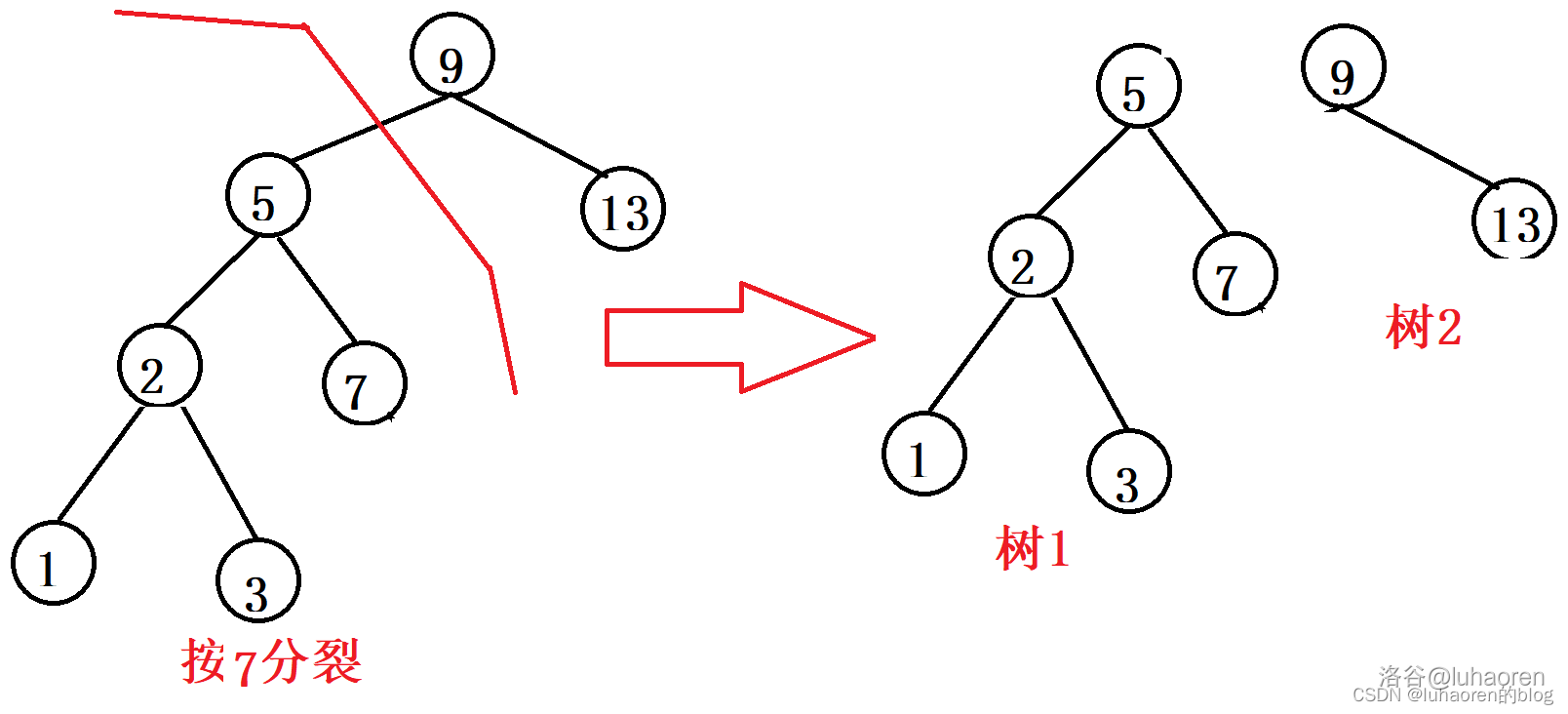
再按分裂成两棵子树(树3和树4)。
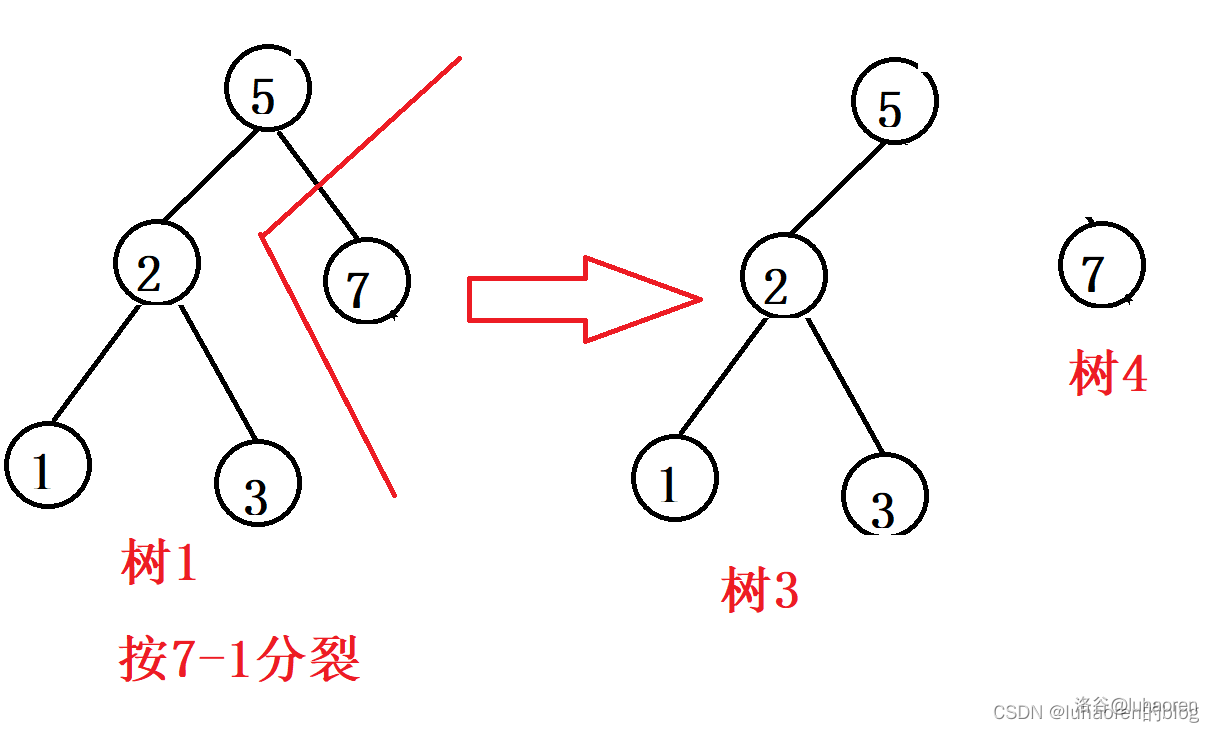
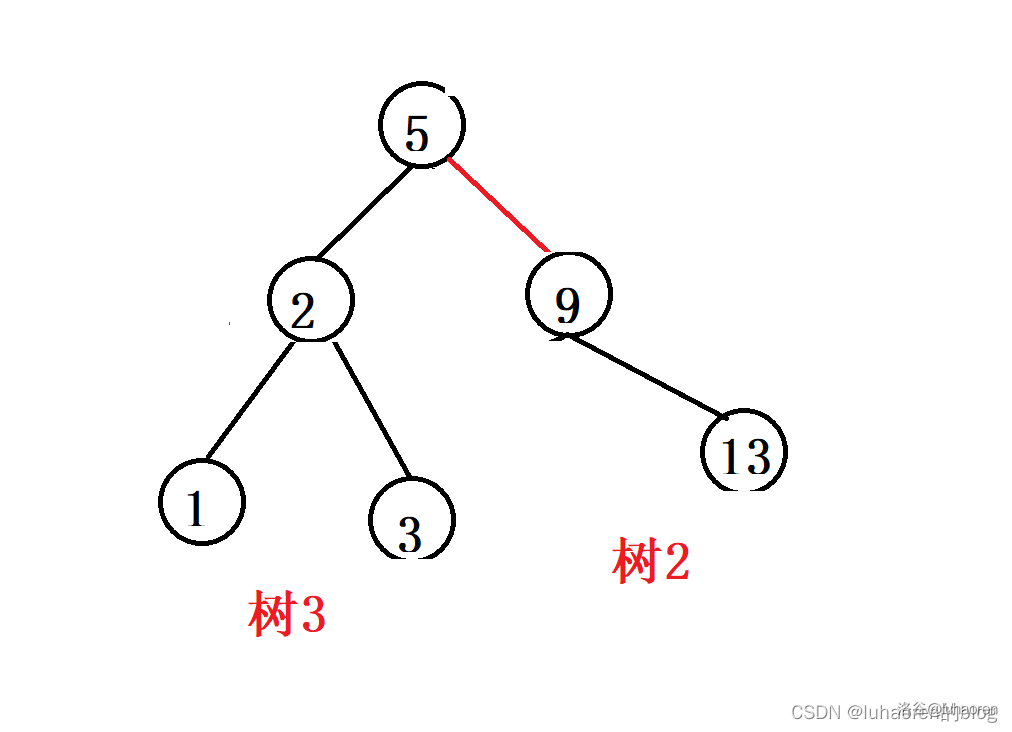
此时树4的根就是我们要找的,把树4的根挑出去,然后合并树342即可。
删除代码
1 | |
查询一个数的排名
排名的定义是"小于这个数的个数"。
按照定义,按分裂,左子树的大小就是排名。
1 | |
查询排名为k的数
这个操作无法用按权值分裂来解决,一般来说有两种写法,一种是使用按大小分裂的方法,分裂出前k个数;另一种是二分解决,这里给出后者的代码。
查询第k大代码
1 | |
前驱和后继
前驱
前驱定义为小于的最大的数,按照定义,我们按分裂,左子树最大的一个数(即)就是的前驱。
求前驱代码
1 | |
后继
同理,按照分裂,右子树的最小值就是的后继。
求后继代码
1 | |
维护区间
区间操作一般由线段树维护,但是,有些问题(如区间翻转)用线段树维护就比较麻烦,那么该用什么维护呢?
平衡树。
事实上,平衡树除了可以作为”排序树“,也可以作为”区间树“,以在数列中的序号为权值建一棵平衡树(这颗平衡树的中序遍历就是原数列),就可以轻易地修改和查询一段区间的信息。
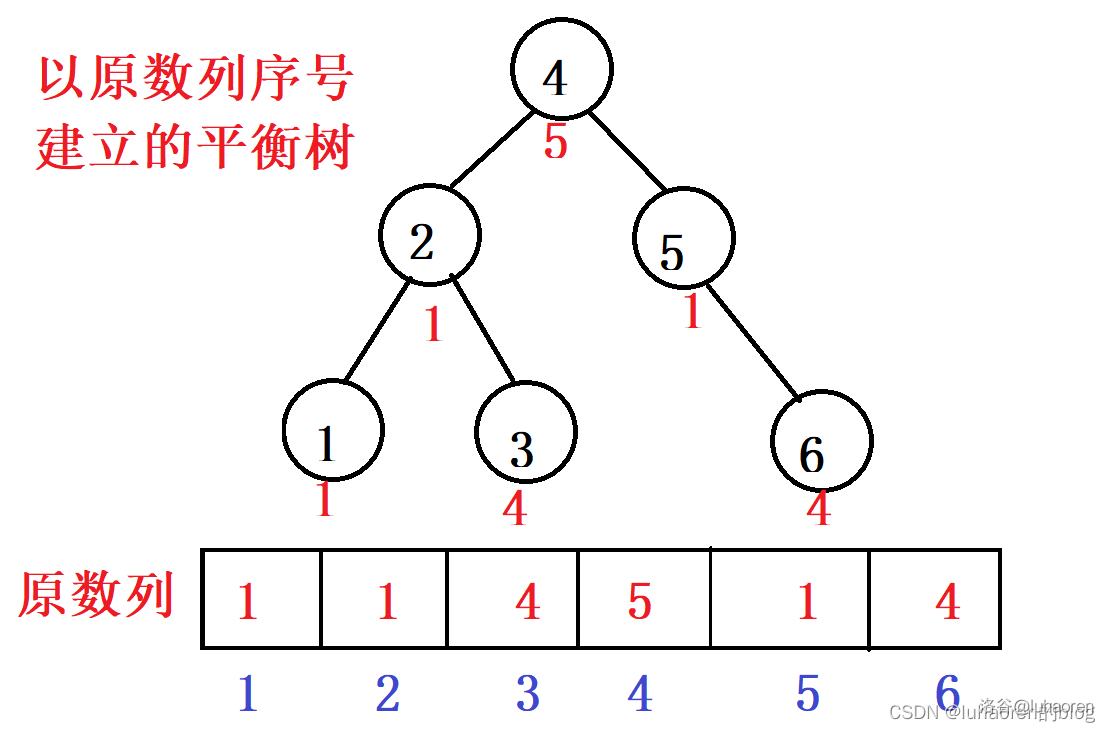
那么我们如何提取出一段区间呢?如果按值分裂,分裂后的操作很可能不符合平衡树性质(如区间翻转),所以我们用到了另一种分裂方式——按大小(排名)分裂。
假如有一个区间,那么先按照分裂成树1和树2,在把树1按分裂成数3和树4,那么区间就是树4所表示的区间。
于是我们就可以修改或者查询树4的信息了!
区间翻转
FHQtreap如何实现区间翻转?
假如有一个序列,我们想翻转区间。

先把[2,5]分裂出来。
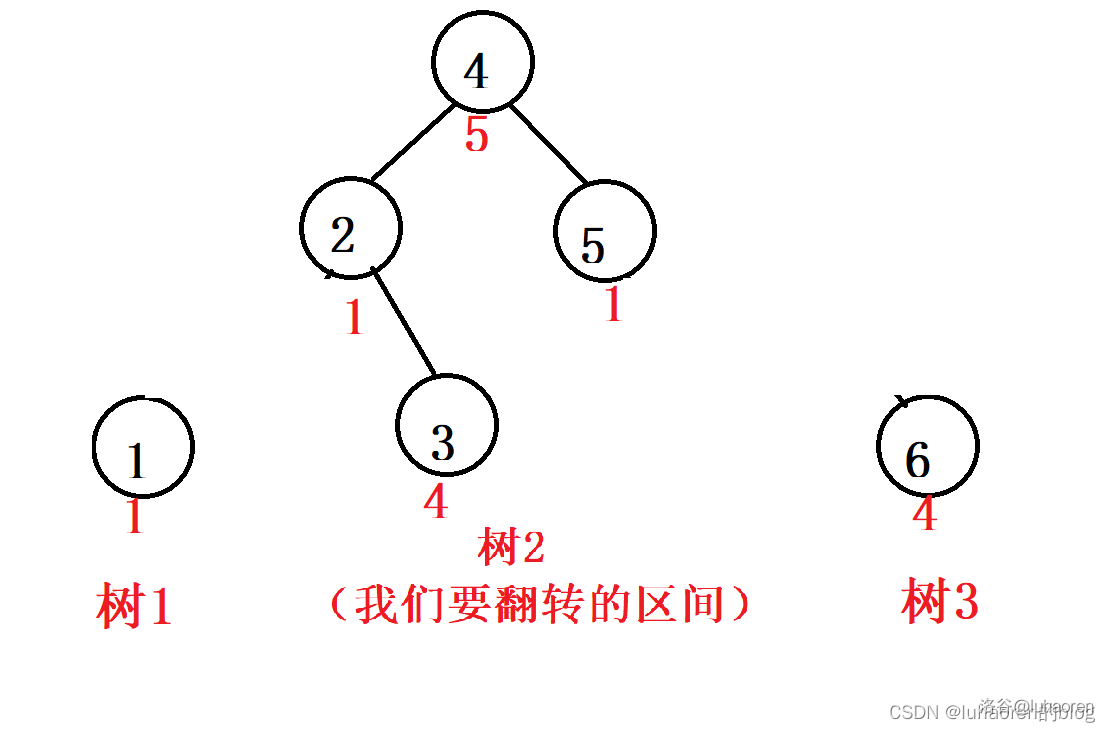
你会发现,所谓区间翻转,就是把树2自顶向下交换左右子树。
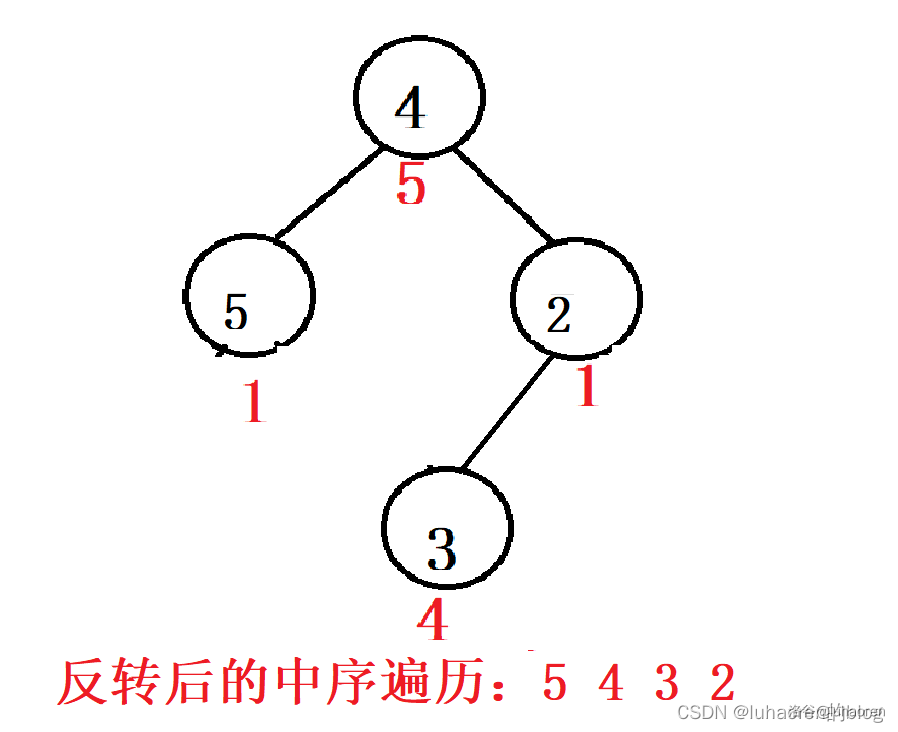
所以就可以用分裂区间自顶向下交换左右子树合并,来维护一段区间的翻转。
但是如果要依次交换这段区间内的每一个左右子树,时间复杂度就会达到,所以我们可以使用懒标记的方式(默认你会)维护。
给要翻转的区间树打上标记,再合并进去,这样就不影响复杂度了!
具体实现见例题·文艺平衡树。
习题
P3369 普通平衡树
模板题,没什么好讲的。
AC代码
1 | |
P1486 郁闷的出纳员
设置一个把工资的调整记录下来。
操作插入新节点时直接插入。
操作时,先改,然后把小于的删掉(这个用fhq做就很方便)
输出的时候别忘了加上。
AC代码(古早时期的代码,码风可能有点差别)
1 | |
P5338 甲苯先生的滚榜
题目要求排序时有两个关键词,用平衡树怎么做呢?
正常使用sort或者优先队列的时候,如果有多个关键词,我们一般会使用重载运算符,而这种多关键词的平衡树问题,我们也可以使用重载运算符,注意要重载和两个运算符。
AC代码
1 | |
P3850 书架
每次插入一个数,后面每一个数的排名都会,可以把排名当成权值,每次插入就用懒标记给后面的数。
注意要保存一个书名的映射(最好直接把书名放到结构体里)
AC代码
1 | |
P3391 文艺平衡树
平衡树区间翻转的模板,我们刚刚已经讲过,直接放代码。
AC代码
1 | |
P4146 序列终结者
平衡树维护区间信息的模板题。
大意是要维护区间最大值,另外要维护区间加和区间翻转。
维护两个懒标记即可,每个节点维护一个最大值,表示当前子树内最大的数。
AC代码
1 | |
P4008 文本编辑器
删除区间,插入区间,输出区间。
这题的输入比较坑,需要注意。
AC代码
1 | |
P3372 【模板】线段树 1
达成成就,用线段树写平衡树,用平衡树写线段树……
AC代码
1 | |
P3380 二逼平衡树(树套树)
这种动态的区间排名问题一般用树套树(线段树套平衡树)解决。
树套树,就是先建一颗平衡树,在每个节点内建一颗平衡树,插入这个区间内的所有树,均摊空间复杂度大概是
查询在区间内的排名,可以在所有包含区间内找小于的数的个数,都加起来在。时间复杂度。
修改某一位值上的数值,找所有包含这这个数的节点,在这些节点上删去这个数,在插入新的数。时间复杂度也是。
查询在区间内的前驱,在所有包含区间内找的前驱,取最大值;同理,后继就是取最小值了。时间复杂度是。
唯一复杂的是查询区间内排名为的值,我们可以用二分答案的方法,在的范围内二分,判断这个数排名是不是,时间复杂度是。
树套树写起来比较复杂,可以锻炼码力和调试能力(我当时调了两周)
AC代码
1 | |